练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    若两个多边形的边数之比是1：2，内角和度数之比为1：3，求这两个多边形的边数．
    考点：多边形内角与外角
    专题：
    分析：设多边形的边数为n，则另一个为2n，分别表示出两个多边形的内角和得到有关n的方程求解即可．
    解答：解：∵两个多边形的边数之比为1：2，
    ∴设多边形的边数为n，则另一个为2n，
    ∵内角和度数之比为1：3，
    ∴（n-2）：2n-2=1：3
    解得：n=4，
    ∴2n=8．
    故这两个多边形的边数分别为：4，8．
    点评：本题考查了多边形的内角与外角，正确的设出边数并表示出其内角和是解决本题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    若多项式a2+2kab与b2-6ab的和不含ab项，则k=
     
    ．如图，点M，N，P是线段AB的四等分点，则BM是AM的
     
    倍．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    -
    2xy
    5
    的系数为（　　）
    A、
    1
    2
    B、-2
    C、
    1
    2
    D、-
    2
    5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    光年天文学中的距离单位，1光年大约是9500000000000km，用科学记数法表示为（　　）
    A、950×1010km
    B、95×1012km
    C、9.5×1012km
    D、0.95×1013km

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知二次函数y=-x2+2x+3．
    （1）求函数图象的顶点坐标，并画出这个函数的图象；
    （2）根据图象，直线写出：
    ①当函数值y为正数时，自变量x的取值范围；
    ②当-2＜x＜2时，函数值y的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

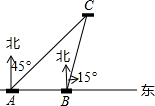    马航失联客机MH370引起全球高度关注，为了搜寻客机残骸，我国派出多艘军舰和海监船到达失事海域进行搜寻，如图，前往南印度洋某海域的我井冈山舰A和昆仑山舰B自西向东航行，B舰在A舰的正东方向，且亮剑保持20海里的距离，某一时刻两舰同时测得在A的东北方向，B的北偏东15°方向有一艘澳方军舰C，求此时舰C与我舰航线AB的距离是多少？（结果保留根号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，正方形ABCD中，点E在边DC上，DE=2，EC=1．把线段AE绕点A旋转，使点E落在直线BC上的点F处，连接DF，则tan∠CDF的值是
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    阅读下列计算过程：
    99×99+199=992+2×99+1=（99+1）2=1002=104
    （1）计算：999×999+1999=
     
    =
     
    =
     
    =
     
    ；
    9999×9999+19999=
     
    =
     
    =
     
    =
     
    ；
    （2）猜想9999999999×9999999999+19999999999等于多少？写出计算过程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

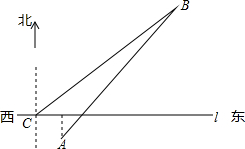    如图，港口A、B位于东西方向航道l的两侧，港口B在A的北偏东45°的方向，航道l上船C与港口B相距100海里，此时在C处测得港口B的方向北偏东55°，已知港口A到航道l距离为13海里，求两港口A、B之间的距离．（参考数据：sin35°≈0.57，cos35°≈0.82，
    		2
    ≈1.41，结果保留整数）

    查看答案和解析>>

    同步练习册答案