
【题目】如图所示,在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a,
b满足 |a+2|+![]() =0,点C的坐标为(0,3).
=0,点C的坐标为(0,3).
(1)求a,b的值及S三角形ABC;
(2)若点M在x轴上,且S三角形ACM=![]() S三角形ABC,试求点M的坐标.
S三角形ABC,试求点M的坐标.

【答案】(1)9(2)(0,0)或(-4,0)
【解析】试题分析:(1)根据绝对值和算术平方根的非负性,求出a、b的值,求得A、B的坐标,然后根据三角形的面积公式求解;
(2)设点M的坐标为(x,0),根据AM的距离和三角形的面积S△ACM=![]() S△ABC可求出AM的值,从而得到M的坐标.
S△ABC可求出AM的值,从而得到M的坐标.
试题解析:(1)∵|a+2|+![]() =0,∴a+2=0,b-4=0.
=0,∴a+2=0,b-4=0.
∴a=-2,b=4.
∴点A(-2,0),点B(4,0).
又∵点C(0,3),∴AB=|-2-4|=6,CO=3.
∴S三角形ABC=![]() AB·CO=
AB·CO=![]() ×6×3=9.
×6×3=9.
(2)设点M的坐标为(x,0),
则AM=|x-(-2)|=|x+2|.
又∵S△ACM=![]() S△ABC,
S△ABC,
∴![]() AM·OC=
AM·OC=![]() ×9,
×9,
∴![]() |x+2|×3=3.
|x+2|×3=3.
∴|x+2|=2.即x+2=±2,
解得x=0或-4,
所以点M的坐标为(0,0)或(-4,0)


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】如图:

(1)如果∠1=∠B,那么_______∥_______,根据是__________________________;
(2)如果∠3=∠D,那么_______∥_______,根据是__________________________;
(3)如果要使BE∥DF,必须∠1=∠_______,根据是_________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列语句中,是真命题的是( )
A.相等的角是对顶角
B.同旁内角互补
C.过一点不只有一条直线与已知直线垂直
D.对于直线 a、b、c,如果 b∥a,c∥a,那么 b∥c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC, 点M在△ABC内,点P在线段MC上,∠ABP=2∠ACM.

(1)若∠PBC=10°,∠BAC=80°,求∠MPB的值
(2)若点M在底边BC的中线上,且BP=AC,试探究∠A与∠ABP之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AC=BC,∠C=90°,点D是AB的中点.
(1)如图1,若点E、F分别是AC、BC上的点,且AE=CF,请判别△DEF的形状,并说明理由;
(2)若点E、F分别是CA、BC延长线上的点,且AE=CF,则(1)中的结论是否仍然成立?请
说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
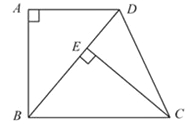
【题目】如图,已知四边形ABCD是梯形,AD∥BC,∠A=90°,BC=BD,CE⊥BD,垂足为E.
(1)求证:△ABD≌△ECB;
(2)若∠DBC=50°,求∠DCE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°

(1)请判断AB与CD的位置关系并说明理由;
(2)如图2,在(1)的结论下,当∠E=90°保持不变,移动直角顶点E,使∠MCE=∠ECD,当直角顶点E点移动时,问∠BAE与∠MCD是否存在确定的数量关系?

(3)如图3,在(1)的结论下,P为线段AC上一定点,点Q为直线CD上一动点,当点Q在射线CD上运动时(点C除外)∠CPQ+∠CQP与∠BAC有何数量关系? (2、3小题只需选一题说明理由)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com