
【题目】如图所示,在不等边![]() 中,
中,![]() ,
,![]() ,AB的垂直平分线交BC边于点E,AC的垂直平分线交BC边于点N.
,AB的垂直平分线交BC边于点E,AC的垂直平分线交BC边于点N.
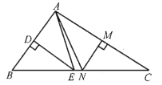
(1)若BC边长为整数,则![]() 的周长为_________.
的周长为_________.
(2)①若![]() ,则
,则![]() 的度数为_________.
的度数为_________.
②若![]() ,则
,则![]() 的度数为_________.
的度数为_________.
③若![]() ,请直接写出
,请直接写出![]() 与
与![]() 之间的数量关系,并画出相应的图形.
之间的数量关系,并画出相应的图形.
【答案】(1)4 ;(2)①![]() ,②
,②![]() ;③
;③![]()
【解析】
(1)根据垂直平分线定理可得AE=BE,AN=CN,即△AEN的周长等于BC,再根据三角形周长定理即可解得.
(2)①由AE=BE,AN=CN可得∠B=∠BAE,∠C=∠CAN,已知∠BAC=70°,则∠B+∠C=180°-70°=110°,则∠CAN+∠BAE=110°,即可求得![]() 的度数.
的度数.
②根据①的解题方法即可解答.
③分两种情况进行解答:![]() 为钝角和若
为钝角和若![]() 为锐角,根据垂直平分线的定理进行作图求证.
为锐角,根据垂直平分线的定理进行作图求证.
(1)![]() AB的垂直平分线交BC边于点E,AC的垂直平分线交BC边于点N;
AB的垂直平分线交BC边于点E,AC的垂直平分线交BC边于点N;
![]() AE=BE,AN=CN;
AE=BE,AN=CN;
![]() △AEN的周长=BC
△AEN的周长=BC
![]() ,
,![]()
![]()
![]() BC=4
BC=4
(2)① ![]() AE=BE,AN=CN
AE=BE,AN=CN
![]() ∠B=∠BAE,∠C=∠CAN,
∠B=∠BAE,∠C=∠CAN,
![]() ∠BAC=70°,
∠BAC=70°,
![]() ∠B+∠C=180°-70°=110°,
∠B+∠C=180°-70°=110°,
![]() ∠CAN+∠BAE=110°,
∠CAN+∠BAE=110°,
![]()
![]()
![]()
![]() =110°-70°=40°.
=110°-70°=40°.
②同理可得:
∠B+∠C=180°-100°=80°
![]() ∠CAN+∠BAE=80°
∠CAN+∠BAE=80°
![]()
=100°-80°=20°;
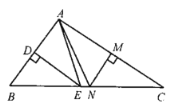
③如图所示,若![]() 为钝角,
为钝角,
则![]() ;
;
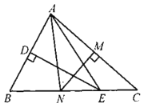
若![]() 为锐角,
为锐角,
则![]() .
.


科目:初中数学 来源: 题型:
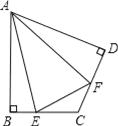
【题目】(1)如图,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是边BC、CD上的点,且∠EAF=![]() ∠BAD.求证:EF=BE+FD;
∠BAD.求证:EF=BE+FD;
(2)如图,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD上的点,且∠EAF=![]() ∠BAD,(1)中的结论是否仍然成立?
∠BAD,(1)中的结论是否仍然成立?
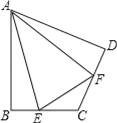
(3)如图,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,且∠EAF=![]() ∠BAD,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.
∠BAD,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
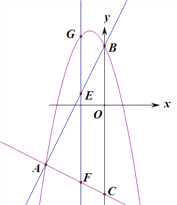
【题目】如图,抛物线y=-x2+bx+c与直线AB交于A(-4,-4),B(0,4)两点,直线AC:y=-![]() x-6交y轴与点C.点E是直线AB上的动点,过点E作EF⊥x轴交AC于点F,交抛物线于点G.
x-6交y轴与点C.点E是直线AB上的动点,过点E作EF⊥x轴交AC于点F,交抛物线于点G.
(1)求抛物线y=-x2+bx+c的表达式;
(2)连接GB、EO,当四边形GEOB是平行四边形时,求点G的坐标;
(3)①在y轴上存在一点H,连接EH、HF,当点E运动到什么位置时,以A、E、F、H为顶点的四边形是矩形?求出此时点E、H的坐标;
②在①的前提下,以点E为圆心,EH长为半径作圆,点M为⊙E上一动点,求![]() AM+CM的最小值.
AM+CM的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】上星期我市某水果价格呈上升趋势,某超市第一次用1000元购进的这种水果很快卖完,第二次又用960元购进该水果,但第二次每千克的进价是第一次进价的1.2倍,购进数量比第一次少了20千克.
(1)求第一次购进这种水果每千克的进价是多少元?
(2)本星期受天气影响,批发市场这种水果的数量有所减少.该超市所购进的数量比上星期所进购的总量减少了4a%,每千克的进价在上星期第二次进价的基础上上涨5a%,结果本星期进货总额比上星期进货总额少16元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
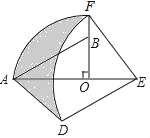
【题目】如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两辆摩托车同时从相距20km的A,B两地出发,相向而行.图中l1,l2分别表示甲、乙两辆摩托车到A地的距离s(km)与行驶时间t(h)的函数关系.则下列说法错误的是
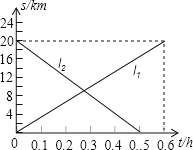
A. 乙摩托车的速度较快
B. 经过0.3小时甲摩托车行驶到A,B两地的中点
C. 经过0.25小时两摩托车相遇
D. 当乙摩托车到达A地时,甲摩托车距离A地![]() km
km
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家具厂生产一种餐桌和椅子,餐桌每张定价为![]() 元,椅子每把定价为
元,椅子每把定价为![]() 元,厂方在开展促销活动期间,向客户提供两种优惠方案:
元,厂方在开展促销活动期间,向客户提供两种优惠方案:
方案一:每买一张餐桌就赠送一把椅子;
方案二:餐桌和椅子都按定价的![]() 付款.
付款.
某餐厅计划添置![]() 张餐桌和
张餐桌和![]() 把椅子.
把椅子.
(1)若![]() ,请用含
,请用含![]() 的代数式分别把两种方案的费用表示出来.
的代数式分别把两种方案的费用表示出来.
(2)已知![]() ,如果两种方案可以同时使用,请帮助餐厅设计一种最省钱的方案.
,如果两种方案可以同时使用,请帮助餐厅设计一种最省钱的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人民商场准备购进甲、乙两种牛奶进行销售,若甲种牛奶的进价比乙种牛奶的进价每件少5元,其用90元购进甲种牛奶的数量与用100元购进乙种牛奶的数量相同.
(1)求甲种牛奶、乙种牛奶的进价分别是多少元?
(2)若该商场购进甲种牛奶的数量是乙种牛奶的3倍少5件,该商场甲种牛奶的销售价格为49元,乙种牛奶的销售价格为每件55元,则购进的甲、乙两种牛奶全部售出后,可使销售的总利润(利润=售价﹣进价)等于371元,请通过计算求出该商场购进甲、乙两种牛奶各自多少件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com