
【题目】如图,抛物线y=![]() x2+mx+n与直线y=﹣
x2+mx+n与直线y=﹣![]() x+3交于A,B两点,交x轴与D,C两点,连接AC,BC,已知A(0,3),C(3,0).
x+3交于A,B两点,交x轴与D,C两点,连接AC,BC,已知A(0,3),C(3,0).
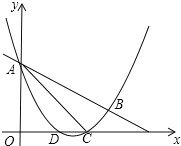
(Ⅰ)求抛物线的解析式和tan∠BAC的值;
(Ⅱ)在(Ⅰ)条件下,P为y轴右侧抛物线上一动点,连接PA,过点P作PQ⊥PA交y轴于点Q,问:是否存在点P使得以A,P,Q为顶点的三角形与△ACB相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
【答案】(Ⅰ)y=![]() x2﹣
x2﹣![]() x+3,
x+3,![]() ;(Ⅱ)满足条件的点P的坐标为(11,36)、(
;(Ⅱ)满足条件的点P的坐标为(11,36)、(![]() ,
,![]() )、(
)、(![]() ,
,![]() ).
).
【解析】
试题分析:(Ⅰ)只需把A、C两点的坐标代入y=![]() x2+mx+n,就可得到抛物线的解析式,然后求出直线AB与抛物线的交点B的坐标,过点B作BH⊥x轴于H,如图1.易得∠BCH=∠ACO=45°,BC=
x2+mx+n,就可得到抛物线的解析式,然后求出直线AB与抛物线的交点B的坐标,过点B作BH⊥x轴于H,如图1.易得∠BCH=∠ACO=45°,BC=![]() ,AC=3
,AC=3![]() ,从而得到∠ACB=90°,然后根据三角函数的定义就可求出tan∠BAC的值;
,从而得到∠ACB=90°,然后根据三角函数的定义就可求出tan∠BAC的值;
(Ⅱ)过点P作PG⊥y轴于G,则∠PGA=90°.设点P的横坐标为x,由P在y轴右侧可得x>0,则PG=x,易得∠APQ=∠ACB=90°.若点G在点A的下方,①当∠PAQ=∠CAB时,△PAQ∽△CAB.此时可证得△PGA∽△BCA,根据相似三角形的性质可得AG=3PG=3x.则有P(x,3﹣3x),然后把P(x,3﹣3x)代入抛物线的解析式,就可求出点P的坐标②当∠PAQ=∠CBA时,△PAQ∽△CBA,同理,可求出点P的坐标;若点G在点A的上方,同理,可求出点P的坐标;
解:(Ⅰ)把A(0,3),C(3,0)代入y=![]() x2+mx+n,得
x2+mx+n,得
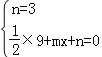 ,
,
解得: .
.
∴抛物线的解析式为y=![]() x2﹣
x2﹣![]() x+3.
x+3.
联立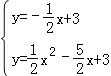 ,
,
解得:![]() 或
或![]() ,
,
∴点B的坐标为(4,1).
过点B作BH⊥x轴于H,如图1.∵C(3,0),B(4,1),
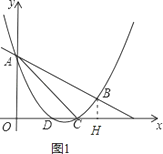
∴BH=1,OC=3,OH=4,CH=4﹣3=1,∴BH=CH=1.
∵∠BHC=90°,∴∠BCH=45°,BC=![]() .
.
同理:∠ACO=45°,AC=3![]() ,
,
∴∠ACB=180°﹣45°﹣45°=90°,
∴tan∠BAC=![]() =
=![]() =
=![]() ;
;
(Ⅱ)(1)存在点P,使得以A,P,Q为顶点的三角形与△ACB相似.
过点P作PG⊥y轴于G,则∠PGA=90°.
设点P的横坐标为x,由P在y轴右侧可得x>0,则PG=x.
∵PQ⊥PA,∠ACB=90°,∴∠APQ=∠ACB=90°.
若点G在点A的下方,
①如图2①,当∠PAQ=∠CAB时,则△PAQ∽△CAB.
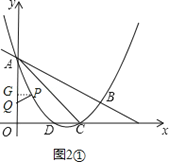
∵∠PGA=∠ACB=90°,∠PAQ=∠CAB,∴△PGA∽△BCA,
∴![]() =
=![]() =
=![]() .
.
∴AG=3PG=3x.
则P(x,3﹣3x).把P(x,3﹣3x)代入y=![]() x2﹣
x2﹣![]() x+3,得:
x+3,得:![]() x2﹣
x2﹣![]() x+3=3﹣3x,
x+3=3﹣3x,
整理得:x2+x=0,解得:x1=0(舍去),x2=﹣1(舍去).
②如图2②,当∠PAQ=∠CBA时,则△PAQ∽△CBA.
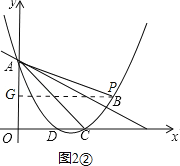
同理可得:AG=![]() PG=
PG=![]() x,则P(x,3﹣
x,则P(x,3﹣![]() x),
x),
把P(x,3﹣![]() x)代入y=
x)代入y=![]() x2﹣
x2﹣![]() x+3,得:
x+3,得:![]() x2﹣
x2﹣![]() x+3=3﹣
x+3=3﹣![]() x,
x,
整理得:x2﹣![]() x=0,解得:x1=0(舍去),x2=
x=0,解得:x1=0(舍去),x2=![]() ,∴P(
,∴P(![]() ,
,![]() );
);
若点G在点A的上方,
①当∠PAQ=∠CAB时,则△PAQ∽△CAB,
同理可得:点P的坐标为(11,36).
②当∠PAQ=∠CBA时,则△PAQ∽△CBA.
同理可得:点P的坐标为P(![]() ,
,![]() ).
).
综上所述:满足条件的点P的坐标为(11,36)、(![]() ,
,![]() )、(
)、(![]() ,
,![]() ).
).


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:初中数学 来源: 题型:
【题目】某校从甲、乙两名优秀选手中选一名选手参加全市中学生田径百米比赛.该校预先对这两名选手测试了8次,测试成绩如下表:
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
选手甲的成绩/秒 | 12.1 | 12.2 | 13 | 12.5 | 13.1 | 12.5 | 12.4 | 12.2 |
选手乙的成绩/秒 | 12 | 12.4 | 12.8 | 13 | 12.2 | 12.8 | 12.3 | 12.5 |
根据测试成绩,请你运用所学过的统计知识做出判断,派哪一位选手参加比赛更好?为什么
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2﹣3x+k与x轴交于A、B两点,与y轴交于点C(0,﹣4).

(1)k= ;
(2)点A的坐标为 ,B的坐标为 ;
(3)设抛物线y=x2﹣3x+k的顶点为M,求四边形ABMC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人骑自行车从甲地到乙地,到达乙地他马上返回甲地.如图反映的是他离甲地的距离s(km)及他骑车的时间t(h)之间的关系,则下列说法正确的是( )
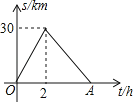
A.甲、乙两地之间的距离为60km
B.他从甲地到乙地的平均速度为30km/h
C.当他离甲地15km时,他骑车的时间为1h
D.若他从乙地返回甲地的平均速度为10km/h,则点A表示的数字为5
查看答案和解析>>
科目:初中数学 来源: 题型:
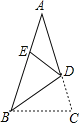
【题目】如图,△ABC中,AB=AC,点D为AC上一点,且BD=BC.将△BCD沿直线BD折叠后,点C落在AB上的点E处,若AE=DE,则∠A的度数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某食品公司产销一种食品,已知每月的生产成本y1与产量x之间是一次函数关系,函数y1与自变量z(kg)的部分对应值如下表:
x(单位:kg) | 10 | 20 | 30 |
y1(单位:/元) | 3030 | 3060 | 3090 |
(1)求y1与x之间的函数关系式;
(2)经过试销发现,这种食品每月的销售收入y2(元)与销量x(kg)之间满足如图所示的函数关系
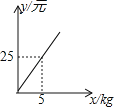
①y2与x之间的函数关系式为 ;
②假设该公司每月生产的该种食品均能全部售出,那么该公司每月至少要生产该种食品多少kg,才不会亏损?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,∠ABC=90°,点F为AB延长线上一点,点E在BC上,BE=BF,连接AE,EF和CF.

(1)求证:△ABE≌△CBF;
(2)若∠CAE=30°,求∠EFC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com