
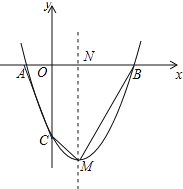
【题目】如图,抛物线y=x2﹣3x+k与x轴交于A、B两点,与y轴交于点C(0,﹣4).

(1)k= ;
(2)点A的坐标为 ,B的坐标为 ;
(3)设抛物线y=x2﹣3x+k的顶点为M,求四边形ABMC的面积.
【答案】(1)k=﹣4;(2)(﹣1,0),(4,0);(3)![]() .
.
【解析】
试题分析:(1)由于抛物线y=x2﹣2x+k与y轴交于点C(0,﹣3),代入解析式中即可求出k;
(2)由y=0,得出方程,解方程即可得出结果;
(3)把抛物线解析式化成顶点式求出顶点M的坐标,四边形ABMC的面积=S△ACN+S△NCM+S△NMB,即可得出结果.
解:(1)把点C(0,﹣4)代入抛物线y=x2﹣3x+k得:k=﹣4,
故答案为:k=﹣4;
(2)∵y=x2﹣3x﹣4,
当y=0时,x2﹣3x﹣4=0,
解得:x=﹣1,或x=4,
∴A(﹣1,0),B(4,0);
故答案为:(﹣1,0),(4,0);
(3)∵y=x2﹣3x﹣4=![]()
∴![]() ,
,
设抛物线的对称轴与x轴交于N,如图所示:
则四边形ABMC的面积=S△ACN+S△NCM+S△NMB
=![]()
=![]()
=![]()
∴四边形ABMC的面积是![]() .
.


科目:初中数学 来源: 题型:
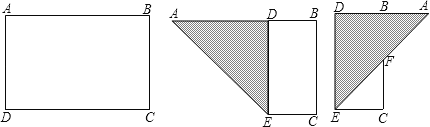
【题目】如图,有一块矩形纸片ABCD,AB=8,AD=6,将纸片折叠,使得AD边落在AB边上,折痕为AE,再将△AED沿DE向右翻折,AE与BC的交点为F,则△CEF的面积为( )
A.![]() B.
B.![]() C.2 D.4
C.2 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() x2+mx+n与直线y=﹣
x2+mx+n与直线y=﹣![]() x+3交于A,B两点,交x轴与D,C两点,连接AC,BC,已知A(0,3),C(3,0).
x+3交于A,B两点,交x轴与D,C两点,连接AC,BC,已知A(0,3),C(3,0).
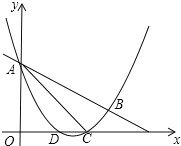
(Ⅰ)求抛物线的解析式和tan∠BAC的值;
(Ⅱ)在(Ⅰ)条件下,P为y轴右侧抛物线上一动点,连接PA,过点P作PQ⊥PA交y轴于点Q,问:是否存在点P使得以A,P,Q为顶点的三角形与△ACB相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】本学期初,我市教育部门对某中学从学生的品德、身心、学习、创新、国际、审美、信息、生活八个方面进行了综合评价,评价小组从八年级学生中选取部分学生针对“信息素养”进行测试,并将测试结果绘制成如下统计图(如图).根据图中信息,解答下列问题:
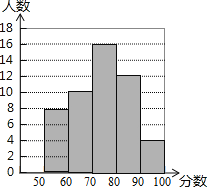
(1)本次选取参加测试的学生人数是 ;
(2)学生“信息素养”得分的中位数是 ;
(3)若把每组中各个分数用这组数据的中间值代替(如30﹣40分的中间值为35分),则参加测试的学生的平均分为 分.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com