练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】有七名同学站成一排照毕业纪念照，其中甲必须站在正中间，并且乙、丙两位同学要站在一起，则不同的站法有（ ）
    A.240种
    B.192种
    C.96种
    D.48种

    【答案】B
    【解析】解：分三步：先排甲，有一种方法；再排乙、丙，排在甲的左边或右边各有4种方法；再排其余4人，有A44种方法， 故共有2×4×A44=192（种）．
    故选B．
    分三步：先排甲；再排乙、丙；最后排其余4人，利用分步计数原理，可得结论．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】下列命题中，是真命题的是（ ）

    A. 两条直线被第三条直线所截，同位角相等B. 垂直于同一直线的两直线平行

    C. 相等的角是对顶角D. 平行于同一直线的两直线平行

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】【新知理解】

    如图①，点C在线段AB上，图中共有三条线段AB、AC和BC，若其中有一条线段的长度是另外一条线段长度的2倍，则称点C是线段AB的“巧点”.

    线段的中点__________这条线段的“巧点”；（填“是”或“不是”）.

    若AB = 12cm，点C是线段AB的巧点，则AC=___________cm；

    【解决问题】

    （3） 如图②，已知AB=12cm.动点P从点A出发，以2cm/s的速度沿AB向点B匀速移动：点Q从点B出发，以1cm/s的速度沿BA向点A匀速移动，点P、Q同时出发，当其中一点到达终点时，运动停止，设移动的时间为t（s）.当t为何值时，A、P、Q三点中其中一点恰好是另外两点为端点的线段的巧点？说明理由

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了深化课程改革，省实验积极开展校本课程建设，计划成立“增量阅读”、“趣味数学”、“音乐舞蹈”和“戏剧英语”等多个社团，要求每位学生都自主选择其中一个社团，为此，随机调查了初中部分学生选择社团的意向．并将调查结果绘制成如下统计图表（不完整）：

    选择意向

    增量阅读

    趣味数学

    音乐舞蹈

    戏曲英语

    其他

    所占百分比

    a

    20%

    b

    10%

    5%


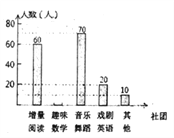
    根据统计图表的信息，解答下列问题：

    (l)求本次抽样调查的学生总人数及a、b的值：

    (2)将条形统计图补充完整；

    (3)若该校共有5000名学生，试估计全校选择“音乐舞蹈”社团的学生人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

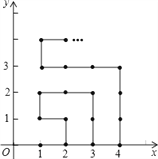
    【题目】16，如图，在平面直角坐标系中，有若干个横坐标分别为整数的点，其顺序按图中“→”方向排列，如（1，0），（2，0），（2，1），（1，1），（1，2），（2，2）…根据这个规律，第2017个点的坐标为

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）如图1，锐角△ABC中，分别以AB、AC为边向外作等边△ABE和等边△ACD，连接BD，CE，试猜想BD与CE的大小关系，并说明理由．

    【深入探究】

    （2）如图2，△ABC中，∠ABC=45°，AB=5cm，BC=3cm，分别以AB、AC为边向外作正方形ABNE和正方形ACMD，连接BD，求BD的长．

    （3）如图3，在（2）的条件下，以AC为直角边在线段AC的左侧作等腰直角△ACD，求BD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在四边形ABCD中，AD∥BC，∠C=90°，BC=CD=8，过点B作EB⊥AB，交CD于点E．若DE=6，则AD的长为（ ）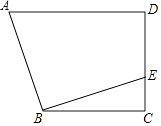

    A.6
    B.8
    C.9
    D.10

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】按图填空，并注明理由．

    ⑴完成正确的证明：如图，已知AB∥CD，求证：∠BED=∠B+∠D

    证明：过E点作EF∥AB（经过直线外一点有且只有一条直线与这条直线平行）

    ∴∠1= （ ）

    ∵AB∥CD（已知）

    ∴EF∥CD（如果两条直线与同一直线平行，那么它们也平行）

    ∴∠2= （ ）

    又∠BED=∠1+∠2

    ∴∠BED=∠B+∠D （等量代换）．

    ⑵如图，在△ABC中，EF∥AD，∠1=∠2，∠BAC=70°．将求∠AGD的过程填写完整．

    解：因为EF∥AD（已知）

    所以∠2=∠3．（ ）

    又因为∠1=∠2，所以∠1=∠3．（等量代换）

    所以AB∥ （ ）

    所以∠BAC+ =180°（ ）．

    又因为∠BAC=70°，所以∠AGD=110°．

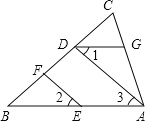
    图⑴ 图⑵

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点P是等边△ABC内一点，连接PA，PB，PC，PA：PB：PC=3：4：5，以AC为边作△AP′C≌△APB，连接PP′，则有以下结论：①△APP′是等边三角形；②△PCP′是直角三角形；③∠APB=150°；④∠APC=105°．其中一定正确的是 ． （把所有正确答案的序号都填在横线上）

    查看答案和解析>>

    同步练习册答案