
【题目】如图,⊙O是△ABC的外接圆,BC是⊙O的直径,∠ABC=30°,过点B作⊙O的切线BD,与CA的延长线交于点D,与半径AO的延长线交于点E,过点A作⊙O的切线AF,与直径BC的延长线交于点F.
(1)求证:△ACF∽△DAE;
(2)若S△AOC= ![]() ,求DE的长;
,求DE的长;
(3)连接EF,求证:EF是⊙O的切线.
【答案】
(1)
证明:∵BC是⊙O的直径,
∴∠BAC=90°,
∵∠ABC=30°,
∴∠ACB=60°
∵OA=OC,
∴∠AOC=60°,
∵AF是⊙O的切线,
∴∠OAF=90°,
∴∠AFC=30°,
∵DE是⊙O的切线,
∴∠DBC=90°,
∴∠D=∠AFC=30,
∵∠DAE=ACF=120°,
∴△ACF∽△DAE;
(2)
∵∠ACO=∠AFC+∠CAF=30°+∠CAF=60°,
∴∠CAF=30°,
∴∠CAF=∠AFC,
∴AC=CF
∴OC=CF,
∵S△AOC= ![]() ,
,
∴S△ACF= ![]() ,
,
∵∠ABC=∠AFC=30°,
∴AB=AF,
∵AB= ![]() BD,
BD,
∴AF= ![]() BD,
BD,
∴∠BAE=∠BEA=30°,
∴AB=BE=AF,
∴ ![]() =
= ![]() ,
,
∵△ACF∽△DAE,
∴ ![]() =(
=( ![]() )2=
)2= ![]() ,
,
∴S△DAE= ![]() ,
,
过A作AH⊥DE于H,
∴AH= ![]() DH=
DH= ![]() DE,
DE,
∴S△ADE= ![]() DEAH=
DEAH= ![]() ×
× ![]() DE2=
DE2= ![]() ,
,
∴DE= ![]() ;
;
(3)
∵∠EOF=∠AOB=120°,
在△AOF与△BOE中,  ,
,
∴△AOF≌△BEO,
∴OE=OF,
∴∠OFG= ![]() (180°﹣∠EOF)=30°,
(180°﹣∠EOF)=30°,
∴∠AFO=∠GFO,
过O作OG⊥EF于G,
∴∠OAF=∠OGF=90°,
在△AOF与△OGF中,  ,
,
∴△AOF≌△GOF,
∴OG=OA,
∴EF是⊙O的切线.
【解析】(1)根据圆周角定理得到∠BAC=90°,根据三角形的内角和得到∠ACB=60°根据切线的性质得到∠OAF=90°,∠DBC=90°,于是得到∠D=∠AFC=30°由相似三角形的判定定理即可得到结论;(2)根据S△AOC= ![]() ,得到S△ACF=
,得到S△ACF= ![]() ,通过△ACF∽△DAE,求得S△DAE=
,通过△ACF∽△DAE,求得S△DAE= ![]() ,过A作AH⊥DE于H,解直角三角形得到AH=
,过A作AH⊥DE于H,解直角三角形得到AH= ![]() DH=
DH= ![]() DE,由三角形的面积公式列方程即可得到结论;(3)根据全等三角形的性质得到OE=OF,根据等腰三角形的性质得到∠OFG=
DE,由三角形的面积公式列方程即可得到结论;(3)根据全等三角形的性质得到OE=OF,根据等腰三角形的性质得到∠OFG= ![]() (180°﹣∠EOF)=30°,于是得到∠AFO=∠GFO,过O作OG⊥EF于G,根据全等三角形的性质得到OG=OA,即可得到结论.
(180°﹣∠EOF)=30°,于是得到∠AFO=∠GFO,过O作OG⊥EF于G,根据全等三角形的性质得到OG=OA,即可得到结论.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】(1)如图①,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备开展“阳光体育活动”,决定开设以下体育活动项目:足球、乒乓球、篮球和羽毛球,要求每位学生必须且只能选择一项,为了解选择各种体育活动项目的学生人数,随机抽取了部分学生进行调查,并将通过调查获得的数据进行整理,绘制出以下两幅不完整的统计图,请根据统计图回答问题: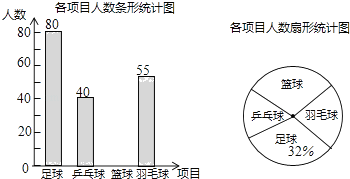
(1)这次活动一共调查了名学生;
(2)补全条形统计图;
(3)在扇形统计图中,选择篮球项目的人数所在扇形的圆心角等于度;
(4)若该学校有1500人,请你估计该学校选择足球项目的学生人数约是人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(11分)阳泉同学参加周末社会实践活动,到“富乐花乡”蔬菜大棚中收集到20株西红柿秧上小西红柿的个数:32 39 45 55 60 54 60 28 56 41 51 36 44 46 40 53 37 47 45 46
(1)前10株西红柿秧上小西红柿个数的平均数是 ,中位数是 ,众数是 ;
(2)若对这20个数按组距8进行分组,请补全频数分布表及频数分布直方图:
个数分组 | 28≤x<36 | 36≤x<44 | 44≤x<52 | 52≤x<60 | 60≤x<68 |
频数 | 2 | 2 |
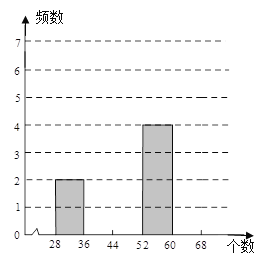
(3)通过频数分布直方图试分析此大棚中西红柿的长势。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD的外侧,作两个等边三角形ADE和DCF,连接AF,BE
(1)请判断:AF与BE的数量关系是 , 位置关系是 .
(2)如图2,若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF,且EA=ED=FD=FC”,第(1)问中的结论是否仍然成立?请作出判断并给予说明
(3)若三角形ADE和DCF为一般三角形,且AE=DF,ED=FC,第(1)问中的结论都能成立吗?请直接写出你的判断.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,过点A作AH⊥EF,垂足为H.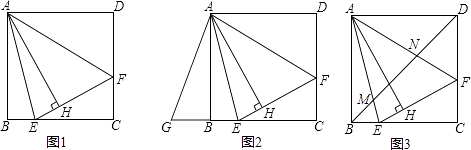
(1)如图2,将△ADF绕点A顺时针旋转90°得到△ABG.
①求证:△AGE≌△AFE;
②若BE=2,DF=3,求AH的长.
(2)如图3,连接BD交AE于点M,交AF于点N.请探究并猜想:线段BM,MN,ND之间有什么数量关系?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com