
【题目】如图,以点O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P为切点,AB=12 ![]() ,OP=6,则劣弧AB的长为 .
,OP=6,则劣弧AB的长为 . 
【答案】8π
【解析】解:连接OA、OB,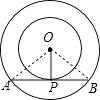
∵AB为小⊙O的切线,
∴OP⊥AB,
∴AP=BP= ![]() AB=6
AB=6 ![]() ,
,
∵ ![]() =
= ![]() ,
,
∴∠AOP=60°,
∴∠AOB=120°,∠OAP=30°,
∴OA=2OP=12,
∴劣弧AB的长为: ![]() =
= ![]() =8π.
=8π.
所以答案是:8π.
【考点精析】关于本题考查的切线的性质定理和弧长计算公式,需要了解切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径;若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的才能得出正确答案.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
【题目】(1)已知等腰三角形的一边长等于8cm,一边长等于9cm,求它的周长;
(2)等腰三角形的一边长等于6cm,周长等于28cm,求其他两边的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,分别作其内角∠ACB与外角∠DAC的角平分线,且两条角平分线所在的直线交于点E
(1)填空:①如图1,若∠B=60°,则∠E= ;
②如图2,若∠B=90°,则∠E= ;
(2)如图3,若∠B=α,求∠E的度数;
(3)如图4,仿照(2)中的方法,在(2)的条件下分别作∠EAB与∠ECB的角平分线,且两条角平分线交于点G,求∠G的度数.
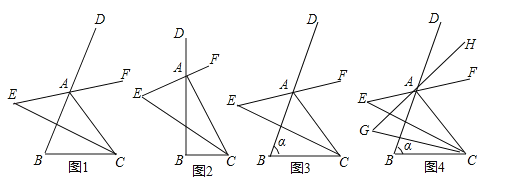
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为a与b、对角线长为c的长方形纸片ABCD,绕点C顺时针旋转90°得到长方形FGCE,连接AF.通过用不同方法计算梯形ABEF的面积可验证勾股定理,请你写出验证的过程.
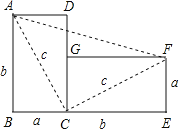
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,BC是⊙O的直径,∠ABC=30°,过点B作⊙O的切线BD,与CA的延长线交于点D,与半径AO的延长线交于点E,过点A作⊙O的切线AF,与直径BC的延长线交于点F.
(1)求证:△ACF∽△DAE;
(2)若S△AOC= ![]() ,求DE的长;
,求DE的长;
(3)连接EF,求证:EF是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了提升初中学生学习数学的兴趣,培养学生的创新精神,举办“玩转数学”比赛.现有甲、乙、丙三个小组进入决赛,评委从研究报告、小组展示、答辩三个方面为各小组打分,各项成绩均按百分制记录.甲、乙、丙三个小组各项得分如表:
小组 | 研究报告 | 小组展示 | 答辩 |
甲 | 91 | 80 | 78 |
乙 | 81 | 74 | 85 |
丙 | 79 | 83 | 90 |
(1)计算各小组的平均成绩,并从高分到低分确定小组的排名顺序;
(2)如果按照研究报告占40%,小组展示占30%,答辩占30%计算各小组的成绩,哪个小组的成绩最高?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了比较市场上甲、乙两种电子钟每日走时误差的情况,从这两种电子钟中,各随机抽取10台进行测试,两种电子钟走时误差的数据如下表(单位:秒):
编号 类型 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 | 九 | 十 |
甲种电子钟 | 1 | -3 | -4 | 4 | 2 | -2 | 2 | -1 | -1 | 2 |
乙种电子钟 | 4 | -3 | -1 | 2 | -2 | 1 | -2 | 2 | -2 | 1 |
(1) 计算甲、乙两种电子钟走时误差的平均数;
(2) 计算甲、乙两种电子钟走时误差的方差;
(3) 根据经验,走时稳定性较好的电子钟质量更优.若两种类型的电子钟价格相同,请问:你买哪种电子钟?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,点E,F分别是边BC,AB上的点,且CE=BF.连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.
(1)请判断:FG与CE的数量关系是 , 位置关系是;
(2)如图2,若点E,F分别是边CB,BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请作出判断并给予证明;
(3)如图3,若点E,F分别是边BC,AB延长线上的点,其它条件不变,(1)中结论是否仍然成立?请直接写出你的判断.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=10,AD=6,点M为AB上的一动点,将矩形ABCD沿某一直线对折,使点C与点M重合,该直线与AB(或BC)、CD(或DA)分别交于点P、Q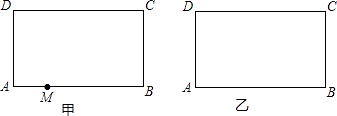
(1)用直尺和圆规在图甲中画出折痕所在直线(不要求写画法,但要求保留作图痕迹)
(2)如果PQ与AB、CD都相交,试判断△MPQ的形状并证明你的结论;
(3)设AM=x,d为点M到直线PQ的距离,y=d2 ,
①求y关于x的函数解析式,并指出x的取值范围;
②当直线PQ恰好通过点D时,求点M到直线PQ的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com