
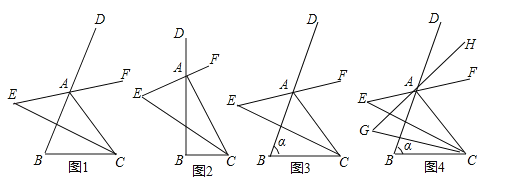
【题目】如图,在△ABC中,分别作其内角∠ACB与外角∠DAC的角平分线,且两条角平分线所在的直线交于点E
(1)填空:①如图1,若∠B=60°,则∠E= ;
②如图2,若∠B=90°,则∠E= ;
(2)如图3,若∠B=α,求∠E的度数;
(3)如图4,仿照(2)中的方法,在(2)的条件下分别作∠EAB与∠ECB的角平分线,且两条角平分线交于点G,求∠G的度数.
【答案】(1)①30°;②45°;(2)∠E=![]() α;(3)∠G =
α;(3)∠G =![]() α.
α.
【解析】
(1)①根据三角形的外角性质可得∠DAC﹣∠ACB=∠B=60°,再根据角平分线的定义可得∠FAC﹣∠ACE=30°,可求∠E的度数;
②根据三角形的外角性质可得∠DAC﹣∠ACB=∠B=90°,再根据角平分线的定义可得∠FAC﹣∠ACE=45°,可求∠E的度数;
(2)根据三角形的外角性质可得∠DAC﹣∠ACB=∠B=![]() α,再根据角平分线的定义可得∠FAC﹣∠ACE=
α,再根据角平分线的定义可得∠FAC﹣∠ACE=![]() α,可求∠E的度数;
α,可求∠E的度数;
(3)根据角平分线的定和义可得三角形的外角性质可得∠G=∠HAC﹣∠ACG=![]() ∠FAC﹣
∠FAC﹣![]() ∠ACE=
∠ACE=![]() (∠FAC﹣∠ACE),可求∠G的度数.
(∠FAC﹣∠ACE),可求∠G的度数.
(1)①∠DAC﹣∠ACB=∠B=60°.
∵EA平分∠DAC,EC平分∠ACB,∴∠FAC=![]() ∠DAC,∠ACE=
∠DAC,∠ACE=![]() ∠ACB,∴∠E=∠FAC﹣∠ACE=
∠ACB,∴∠E=∠FAC﹣∠ACE=![]() ∠B=30°;
∠B=30°;
②∠DAC﹣∠ACB=∠B=60°.
∵EA平分∠DAC,EC平分∠ACB,∴∠FAC=![]() ∠DAC,∠ACE=
∠DAC,∠ACE=![]() ∠ACB,∴∠E=∠FAC﹣∠ACE=
∠ACB,∴∠E=∠FAC﹣∠ACE=![]() ∠B=45°;
∠B=45°;
(2)∠DAC﹣∠ACB=∠B=α.
∵EA平分∠DAC,EC平分∠ACB,∴∠FAC=![]() ∠DAC,∠ACE=
∠DAC,∠ACE=![]() ∠ACB,∴∠E=∠FAC﹣∠ACE=
∠ACB,∴∠E=∠FAC﹣∠ACE=![]() ∠B=
∠B=![]() α;
α;
(3)∵AG,CG分别是∠EAB与∠ECB的角平分线,∴∠G=∠HAC﹣∠ACG=![]() ∠FAC﹣
∠FAC﹣![]() ∠ACE=
∠ACE=![]() (∠FAC﹣∠ACE)=
(∠FAC﹣∠ACE)=![]() ×
×![]() ∠B=
∠B=![]() α.
α.


科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AB=AC,∠A=60°,BD⊥AC于点D,DG∥AB,DG交BC于点G,点E在BC的延长线上,且CE=CD.
(1)求∠ABD和∠BDE的度数;
(2)写出图中的等腰三角形(写出3个即可).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,边长为2的正方形OABC的顶点A、C分别在x轴、y轴的正半轴上,二次函数y=﹣ ![]() x2+bx+c的图象经过B、C两点.
x2+bx+c的图象经过B、C两点.
(1)求该二次函数的解析式;
(2)结合函数的图象探索:当y>0时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC是等腰直角三角形,∠BAC=90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.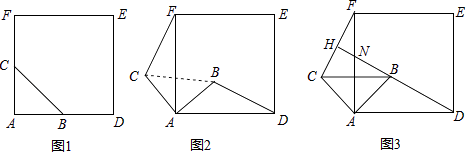
(1)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明,若不成立,请说明理由;
(2)当△ABC绕点A逆时针旋转45°时,如图3,延长BD交CF于点H.
①求证:BD⊥CF;
②当AB=2,AD=3 ![]() 时,求线段DH的长.
时,求线段DH的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com