
【题目】画图并填空,如图:方格纸中每个小正方形的边长都为1,△ABC的顶点都在方格纸的格点上,将△ABC经过一次平移后得到△A'B'C'.图中标出了点C的对应点C'.
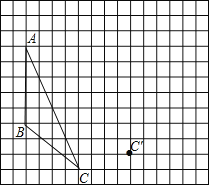
(1)请画出平移后的△A'B'C';
(2)若连接AA',BB',则这两条线段的关系是 ;
(3)利用网格画出△ABC中AC边上的中线BD以及AB边上的高CE;
(4)线段AB在平移过程中扫过区域的面积为 .
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】(探究)如图①,∠AFH和∠CHF的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.
(1)若∠AFH=60°,∠CHF=50°,则∠EOF=_____度,∠FOH=_____度.
(2)若∠AFH+∠CHF=100°,求∠FOH的度数.
(拓展)如图②,∠AFH和∠CHI的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.若∠AFH+∠CHF=α,直接写出∠FOH的度数.(用含a的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直线y= ![]() x+2与x轴交于点A,与y轴交于点C,抛物线y=ax2+4ax+b经过A.C两点,且与x轴交于另一点B.
x+2与x轴交于点A,与y轴交于点C,抛物线y=ax2+4ax+b经过A.C两点,且与x轴交于另一点B.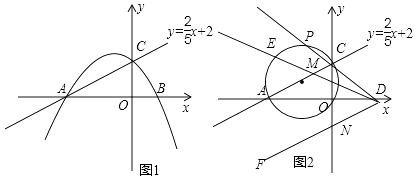
(1)求抛物线的解析式;
(2)若点Q在抛物线上,且△AQC与△BQC面积相等,求点Q的坐标;
(3)如图2,P为△AOC外接圆上弧ACO的中点,直线PC交x轴于点D,∠EDF=∠ACO,当∠EDF绕点D旋转时,DE交直线AC于点M,DF交y轴负半轴于点N.请你探究:CN﹣CM的值是否发生变化?若不变,求出其值;若变化,求出变化范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司有![]() 、
、![]() 两种型号的客车共20辆,它们的载客量、每天的租金如下表所示.已知在20辆客车都坐满的情况下,共载客720人.
两种型号的客车共20辆,它们的载客量、每天的租金如下表所示.已知在20辆客车都坐满的情况下,共载客720人.
A型号客车 | B型号客车 | |
载客量(人/辆) | 45 | 30 |
租金(元/辆) | 600 | 450 |
(1)求![]() 、
、![]() 两种型号的客车各有多少辆?
两种型号的客车各有多少辆?
(2)某中学计划租用![]() 、
、![]() 两种型号的客车共8辆,同时送七年级师生到沙家浜参加社会实践活动,已知该中学租车的总费用不超过4600元. 求最多能租用多少辆A型号客车?
两种型号的客车共8辆,同时送七年级师生到沙家浜参加社会实践活动,已知该中学租车的总费用不超过4600元. 求最多能租用多少辆A型号客车?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点E为矩形ABCD外一点,连接AE,DE,且AE=DE,连接EB,EC分别与AD相交于点F,G.
(1)如图1,求证:∠ABE=∠DCE;
(2)如图2,若△BCE是等边三角形,且AE=AB,在不添加任何辅助线的情况下,请直接写出图2中四对全等的钝角三角形.
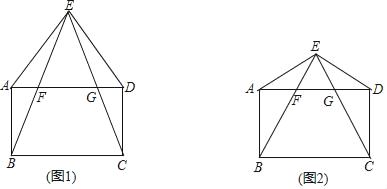
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一种折叠椅,忽略其支架等的宽度,得到他的侧面简化结构图(图2),支架与坐板均用线段表示,若座板DF平行于地面MN,前支撑架AB与后支撑架AC分别与座板DF交于点E、D,现测得DE=20厘米,DC=40厘米,∠AED=58°,∠ADE=76°. 
(1)求椅子的高度(即椅子的座板DF与地面MN之间的距离)(精确到1厘米)
(2)求椅子两脚B、C之间的距离(精确到1厘米)(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60,sin76°≈0.97.cos76°≈0.24,tan76°≈4.00)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com