
【题目】如图1是一种折叠椅,忽略其支架等的宽度,得到他的侧面简化结构图(图2),支架与坐板均用线段表示,若座板DF平行于地面MN,前支撑架AB与后支撑架AC分别与座板DF交于点E、D,现测得DE=20厘米,DC=40厘米,∠AED=58°,∠ADE=76°. 
(1)求椅子的高度(即椅子的座板DF与地面MN之间的距离)(精确到1厘米)
(2)求椅子两脚B、C之间的距离(精确到1厘米)(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60,sin76°≈0.97.cos76°≈0.24,tan76°≈4.00)
【答案】
(1)解:如图,作DP⊥MN于点P,即∠DPC=90°,
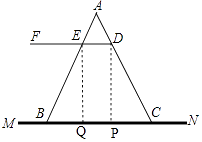
∵DE∥MN,
∴∠DCP=∠ADE=76°,
则在Rt△CDP中,DP=CDsin∠DCP=40×sin76°≈39(cm),
答:椅子的高度约为39厘米
(2)解:作EQ⊥MN于点Q,
∴∠DPQ=∠EQP=90°,
∴DP∥EQ,
又∵DF∥MN,∠AED=58°,∠ADE=76°,
∴四边形DEQP是矩形,∠DCP=∠ADE=76°,∠EBQ=∠AED=58°,
∴DE=PQ=20,EQ=DP=39,
又∵CP=CDcos∠DCP=40×cos76°≈9.6(cm),
BQ= ![]() =
= ![]() ≈24.4(cm),
≈24.4(cm),
∴BC=BQ+PQ+CP=24.4+20+9.6≈54(cm),
答:椅子两脚B、C之间的距离约为54cm
【解析】(1)作DP⊥MN于点P,即∠DPC=90°,由DE∥MN知∠DCP=∠ADE=76°,根据DP=CDsin∠DCP可得答案;(2)作EQ⊥MN于点Q可得四边形DEQP是矩形,知DE=PQ=20,EQ=DP=39,再分别求出BQ、CP的长可得答案.


科目:初中数学 来源: 题型:
【题目】画图并填空,如图:方格纸中每个小正方形的边长都为1,△ABC的顶点都在方格纸的格点上,将△ABC经过一次平移后得到△A'B'C'.图中标出了点C的对应点C'.
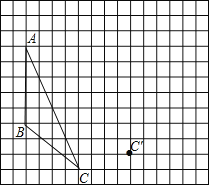
(1)请画出平移后的△A'B'C';
(2)若连接AA',BB',则这两条线段的关系是 ;
(3)利用网格画出△ABC中AC边上的中线BD以及AB边上的高CE;
(4)线段AB在平移过程中扫过区域的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为m的正三角形,D,E,F分别在边AB,BC,CA上,AE,BF交于点P,BF,CD交于点Q,CD,AE交于点R,若 ![]() =
= ![]() =
= ![]() =k(0<k<
=k(0<k< ![]() ).
).
(1)求∠PQR的度数;
(2)求证:△ARD∽△ABE;
(3)求△PQR与△ABC的面积之比(用含k的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某手机专营店代理销售A、B两种型号手机.手机的进价、售价如下表:
型号 | A | B |
进价 | 1800元/部 | 1500元/部 |
售价 | 2070元/部 | 1800元/部 |
(1)第一个月:用54000元购进A、B两种型号的手机,全部售完后获利9450元,求第一个月购进A、B两种型号手机的数量;
(2)第二个月:计划购进A、B两种型号手机共34部,且不超出第一个月购进A、B两种型号的手机总费用,则A型号手机最多能购多少部?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市扶贫办在精准扶贫工作中,组织30辆汽车装运花椒、核桃、甘蓝向外地销售.按计划30辆车都要装运,每辆汽车只能装运同一种产品,且必须装满,根据下表提供的信息,解答以下问题:
产品名称 | 核桃 | 花椒 | 甘蓝 |
每辆汽车运载量(吨) | 10 | 6 | 4 |
每吨土特产利润(万元) | 0.7 | 0.8 | 0.5 |
若装运核桃的汽车为x辆,装运甘蓝的车辆数是装运核桃车辆数的2倍多1,假设30辆车装运的三种产品的总利润为y万元.
(1)求y与x之间的函数关系式;
(2)若装花椒的汽车不超过8辆,求总利润最大时,装运各种产品的车辆数及总利润最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD⊥BC,EF⊥BC,垂足分别为D、F,∠2+∠3=180°,试说明:∠GDC=∠B.请补充说明过程,并在括号内填上相应的理由.
解:∵AD⊥BC,EF⊥BC(已知)
∴∠ADB=∠EFB=90° ,
∴EF∥AD( ),
∴ +∠2=180°( ).
又∵∠2+∠3=180°(已知),
∴∠1=∠3( ),
∴AB∥ ( ),
∴∠GDC=∠B( ).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s。
⑴连接AQ、CP交于点M,在点P、Q运动的过程中,∠CMQ的大小变化吗?若变化,则说明理由,若不变,请直接写出它的度数;
⑵点P、Q在运动过程中,设运动时间为t,当t为何值时,△PBQ为直角三角形?
⑶如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠CMQ的大小变化吗?则说明理由;若不变,请求出它的度数。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料: 由于发展时间早、发展速度快,经过20多年大规模的高速开发建设,北京四环内,甚至五环内可供开发建设的土地资源越来越稀缺,更多的土地供应将集中在五环外,甚至六环外的远郊区县.
据中国经济网2017年2月报道,来自某市场研究院的最新统计,2016年,剔除了保障房后,在北京新建商品住宅交易量整体上涨之时,北京各区域的新建商品住宅交易量则是有涨有跌.其中,昌平、通州、海淀、朝阳、西城、东城六区下跌,跌幅最大的为朝阳区,新建商品住宅成交量比2015年下降了46.82%.而延庆、密云、怀柔、平谷、门头沟、房山、顺义、大兴、石景山、丰台十区的新建商品住宅成交量表现为上涨,涨幅最大的为顺义区,比2015年上涨了118.80%.另外,从环线成交量的占比数据上,同样可以看出成交日趋郊区化的趋势.根据统计,2008年到2016年,北京全市成交的新建商品住宅中,二环以内的占比逐步从3.0%下降到了0.2%;二、三环之间的占比从5.7%下降到了0.8%;三、四环之间的占比从12.3%下降到了2.3%;四、五环之间的占比从21.9%下降到了4.4%.也就是说,整体成交中位于五环之内的新房占比,从2008年的42.8%下降到了2016年的7.7%,下滑趋势非常明显.由此可见,新房市场的远郊化是北京房地产市场发展的大势所趋.(注:占比,指在总数中所占的比重,常用百分比表示)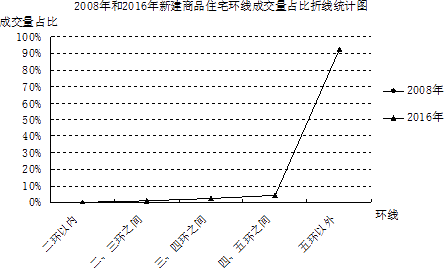
根据以上材料解答下列问题:
(1)补全折线统计图;
(2)根据材料提供的信息,预估 2017年位于北京市五环之内新建商品住宅成交量占比约 , 你的预估理由是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com