
【题目】如图,已知AD⊥BC,EF⊥BC,垂足分别为D、F,∠2+∠3=180°,试说明:∠GDC=∠B.请补充说明过程,并在括号内填上相应的理由.
解:∵AD⊥BC,EF⊥BC(已知)
∴∠ADB=∠EFB=90° ,
∴EF∥AD( ),
∴ +∠2=180°( ).
又∵∠2+∠3=180°(已知),
∴∠1=∠3( ),
∴AB∥ ( ),
∴∠GDC=∠B( ).

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某公司有![]() 、
、![]() 两种型号的客车共20辆,它们的载客量、每天的租金如下表所示.已知在20辆客车都坐满的情况下,共载客720人.
两种型号的客车共20辆,它们的载客量、每天的租金如下表所示.已知在20辆客车都坐满的情况下,共载客720人.
A型号客车 | B型号客车 | |
载客量(人/辆) | 45 | 30 |
租金(元/辆) | 600 | 450 |
(1)求![]() 、
、![]() 两种型号的客车各有多少辆?
两种型号的客车各有多少辆?
(2)某中学计划租用![]() 、
、![]() 两种型号的客车共8辆,同时送七年级师生到沙家浜参加社会实践活动,已知该中学租车的总费用不超过4600元. 求最多能租用多少辆A型号客车?
两种型号的客车共8辆,同时送七年级师生到沙家浜参加社会实践活动,已知该中学租车的总费用不超过4600元. 求最多能租用多少辆A型号客车?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=6,BC=8,点D、M分别在BC、AC上,Rt△BDE、Rt△EFG、Rt△GHI、Rt△IJK、Rt△KMA的斜边都在AB上,则五个小直角三角形的周长和为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两个蓄水池,现将甲池中的水匀速注入乙池.甲、乙两个蓄水池中水的深度![]() (米)与注水时间
(米)与注水时间![]() (小时)之间的关系如图5所示,根据图像提供的信息,回答下列问题:
(小时)之间的关系如图5所示,根据图像提供的信息,回答下列问题:
(1)注水前甲池中水的深度是_____________米.(直接写出答案).
(2)求甲池中水的深度![]() (米)与注水时间
(米)与注水时间![]() (小时)之间的函数关系式;
(小时)之间的函数关系式;
(3)求注水多长时间时,甲、乙两个蓄水池中水的深度相同.
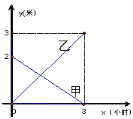
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一种折叠椅,忽略其支架等的宽度,得到他的侧面简化结构图(图2),支架与坐板均用线段表示,若座板DF平行于地面MN,前支撑架AB与后支撑架AC分别与座板DF交于点E、D,现测得DE=20厘米,DC=40厘米,∠AED=58°,∠ADE=76°. 
(1)求椅子的高度(即椅子的座板DF与地面MN之间的距离)(精确到1厘米)
(2)求椅子两脚B、C之间的距离(精确到1厘米)(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60,sin76°≈0.97.cos76°≈0.24,tan76°≈4.00)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三个登山爱好者经常相约去登山,今年1月甲参加了两次登山活动.
(1)1月1日甲与乙同时开始攀登一座900米高的山,甲的平均攀登速度是乙的1.2倍,结果甲比乙早15分钟到达顶峰.求甲的平均攀登速度是每分钟多少米?
(2)1月6日甲与丙去攀登另一座h米高的山,甲保持第(1)问中的速度不变,比丙晚出发0.5小时,结果两人同时到达顶峰,问甲的平均攀登速度是丙的多少倍?(用含h的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ABC、∠ACB的平分线相交于O,MN过点O且与BC平行.△ABC的周长为20,△AMN的周长为12,则BC的长为( )
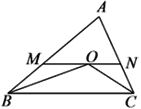
A. 10 B. 16 C. 8 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AB=AC,∠A=120°.
(1)作线段AB的垂直平分线,分别交BC、AB于点M、N(要求用尺规作图,保留作图痕迹,不写作法);
(2)连接AM,判断△AMC的形状,并给予证明;
(3)求证:CM=2BM.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C,D为⊙O上两点,CF⊥AB于点F,CE⊥AD交AD的延长线于点E,且CE=CF. 
(1)求证:CE是⊙O的切线;
(2)连接CD,CB.若AD=CD=a,写出求四边形ABCD面积的思路. 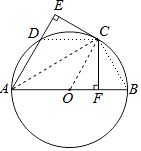
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com