
【题目】如图所示,在△ABC中,AB=AC,∠A=120°.
(1)作线段AB的垂直平分线,分别交BC、AB于点M、N(要求用尺规作图,保留作图痕迹,不写作法);
(2)连接AM,判断△AMC的形状,并给予证明;
(3)求证:CM=2BM.

【答案】(1)见解析;(2)△AMC为直角三角形;(3)证明见解析.
【解析】
(1)尺规作图,要按照规范画图进行,要显示作图痕迹.
(2)明确△ABC各内角的度数,根据垂直平分线的性质,连接AM,即可求出∠MAC的度数;
(3)由(2)知△AMC为直角三角形,得出CM与AM的数量关系即可得出结论;
(1)
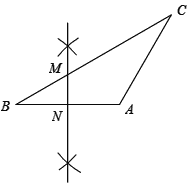
(2)△AMC为直角三角形.
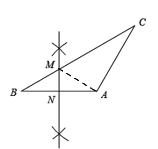
连接AM,则BM=AM,
∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∴∠MAB=∠B=30°,∠MAC=90°,
∴△AMC为直角三角形;
(3)∵∠CAM=90°,∠C=30°,
∴CM=2AM.
∵MN垂直平分AB,
∴AM=BM,
∴CM=2BM.


科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E,∠ADC=70°.
(1)求∠EDC的度数;
(2)若∠ABC=n°,求∠BED的度数(用含n的代数式表示);
(3)将线段BC沿DC方向平移,使得点B在点A的右侧,其他条件不变,画出图形并判断∠BED的度数是否改变,若改变,求出它的度数(用含n的式子表示);若不改变,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD⊥BC,EF⊥BC,垂足分别为D、F,∠2+∠3=180°,试说明:∠GDC=∠B.请补充说明过程,并在括号内填上相应的理由.
解:∵AD⊥BC,EF⊥BC(已知)
∴∠ADB=∠EFB=90° ,
∴EF∥AD( ),
∴ +∠2=180°( ).
又∵∠2+∠3=180°(已知),
∴∠1=∠3( ),
∴AB∥ ( ),
∴∠GDC=∠B( ).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点.若AE=2,当EF+CF取得最小值时,∠ECF的度数为( )

A. 20° B. 25° C. 30° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;
(2)AB=BC+AD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,若P,Q为某个菱形相邻的两个顶点,且该菱形的两条对角线分别与x轴,y轴平行,则称该菱形为点P,Q的“相关菱形”.图1为点P,Q的“相关菱形”的一个示意图. 
已知点A的坐标为(1,4),点B的坐标为(b,0),
(1)若b=3,则R(﹣1,0),S(5,4),T(6,4)中能够成为点A,B的“相关菱形”顶点的是;
(2)若点A,B的“相关菱形”为正方形,求b的值;
(3)⊙B的半径为 ![]() ,点C的坐标为(2,4).若⊙B上存在点M,在线段AC上存在点N,使点M,N的“相关菱形”为正方形,请直接写出b的取值范围.
,点C的坐标为(2,4).若⊙B上存在点M,在线段AC上存在点N,使点M,N的“相关菱形”为正方形,请直接写出b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两支篮球队进行了5场比赛,比赛成绩绘制成了统计图(如图)
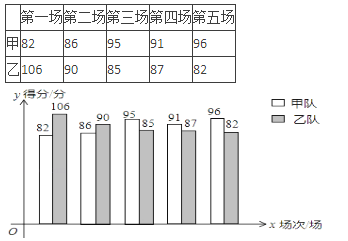
(1)分别计算甲乙两队5场比赛成绩的平均分.
(2)就这5场比赛,分别计算两队成绩的极差;
(3)就这5场比赛,分别计算两队成绩的方差;
(4)如果从两队中选派一支球队参加篮球锦标赛,根据上述统计,从平均分、极差、方差以及获胜场数这四个方面分别进行简要分析,你认为选派哪支球队参赛更能取得好成绩?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=α,AC、BD交于M
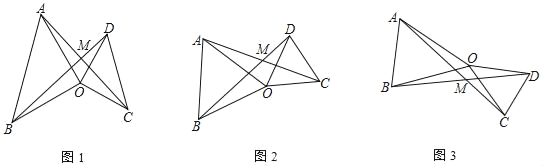
(1)如图1,当α=90°时,∠AMD的度数为 °
(2)如图2,当α=60°时,∠AMD的度数为 °
(3)如图3,当△OCD绕O点任意旋转时,∠AMD与α是否存在着确定的数量关系?如果存在,请你用表示∠AMD,并图3进行证明;若不确定,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com