
【题目】如图,△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=α,AC、BD交于M
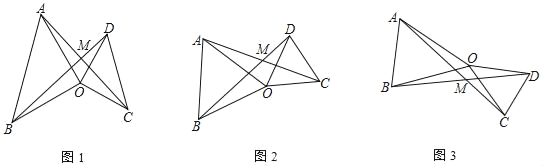
(1)如图1,当α=90°时,∠AMD的度数为 °
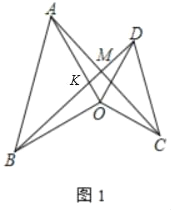
(2)如图2,当α=60°时,∠AMD的度数为 °
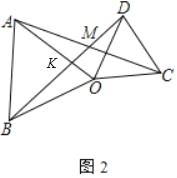
(3)如图3,当△OCD绕O点任意旋转时,∠AMD与α是否存在着确定的数量关系?如果存在,请你用表示∠AMD,并图3进行证明;若不确定,说明理由.
【答案】(1)90;(2)60;(3)∠AMD=180°﹣α,证明详见解析.
【解析】
(1)如图1中,设OA交BD于K.只要证明△BOD≌△AOC,推出∠OBD=∠OAC,由∠AKM=∠BKO,可得∠AMK=∠BOK=90°;
(2)如图2中,设OA交BD于K.只要证明△BOD≌△AOC,推出∠OBD=∠OAC,由∠AKM=∠BKO,推出∠AMK=∠BOK=60°;
(3)如图3中,设OA交BD于K.只要证明△BOD≌△AOC,可得∠OBD=∠OAC,由∠AKO=∠BKM,推出∠AOK=∠BMK=α.可得∠AMD=180°-α.
(1)如图1中,设OA交BD于K.
∵OA=OB,OC=OD,∠AOB=∠COD=α,
∴∠BOD=∠AOC,
∴△BOD≌△AOC,
∴∠OBD=∠OAC,
∵∠AKM=∠BKO,
∴∠AMK=∠BOK=90°.
故答案为90.
(2)如图2中,设OA交BD于K.
∵OA=OB,OC=OD,∠AOB=∠COD=α,
∴∠BOD=∠AOC,
∴△BOD≌△AOC,
∴∠OBD=∠OAC,
∵∠AKM=∠BKO,
∴∠AMK=∠BOK=60°.
故答案为60.
(3)如图3中,设OA交BD于K.
∵OA=OB,OC=OD,∠AOB=∠COD=α,
∴∠BOD=∠AOC,
∴△BOD≌△AOC,
∴∠OBD=∠OAC,
∵∠AKO=∠BKM,
∴∠AOK=∠BMK=α.
∴∠AMD=180°﹣α.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AB=AC,∠A=120°.
(1)作线段AB的垂直平分线,分别交BC、AB于点M、N(要求用尺规作图,保留作图痕迹,不写作法);
(2)连接AM,判断△AMC的形状,并给予证明;
(3)求证:CM=2BM.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C,D为⊙O上两点,CF⊥AB于点F,CE⊥AD交AD的延长线于点E,且CE=CF. 
(1)求证:CE是⊙O的切线;
(2)连接CD,CB.若AD=CD=a,写出求四边形ABCD面积的思路. 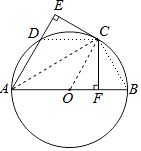
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某健步走运动的爱好者用手机软件记录了某个月(30天)每天健步走的步数(单位:万步),将记录结果绘制成了如图所示的统计图.在每天所走的步数这组数据中,众数和中位数分别是( )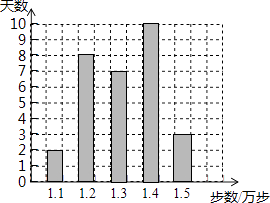
A.1.2,1.3
B.1.3,1.3
C.1.4,1.35
D.1.4,1.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知甲沿周长为300米的环形跑道按逆时针方向跑步,速度为a米/秒,与此同时在甲后面100米的乙也沿该环形跑道按逆时针方向跑步,速度为3米/秒.
(1)若a=1,求甲、乙两人第一次相遇所用的时间;
(2)若a>3,甲、乙两人第一次相遇所用的时间为80秒,试求a的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形,∠BAD的角平分线AF交CD于点E,交BC的延长线于点F. 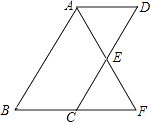
(1)求证:BF=CD;
(2)连接BE,若BE⊥AF,∠BFA=60°,BE=2 ![]() ,求平行四边形ABCD的周长.
,求平行四边形ABCD的周长. 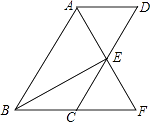
查看答案和解析>>
科目:初中数学 来源: 题型:
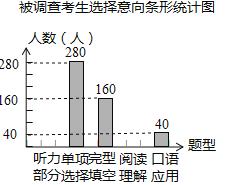
【题目】为了解中考考生最喜欢做哪种类型的英语客观题,2015年志愿者奔赴全市中考各考点对英语客观题的“听力部分、单项选择、完型填空、阅读理解、口语应用”进行了问卷调查,要求每位考生都自主选择其中一个类型,为此随机调查了各考点部分考生的意向.并将调查结果绘制成如图的统计图表(问卷回收率为100%,并均为有效问卷).
被调查考生选择意向统计表

根据统计图表中的信息,解答下列问题:
(1)求本次被调查的考生总人数及a、b、c的值;
(2)将条形统计图补充完整;
(3)全市参加这次中考的考生共有42000人,试估计全市考生中最喜欢做“单项选择”这类客观题的考生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰△ABC中,
(1)如图1,若△ABC为等边三角形,D为线段BC中点,线段AD关于直线AB的对称线段为线段AE,连接DE,则∠BDE的度数为;
(2)若△ABC为等边三角形,点D为线段BC上一动点(不与B,C重合),连接AD并将 线段AD绕点D逆时针旋转60°得到线段DE,连接BE.
①根据题意在图2中补全图形;
②小玉通过观察、验证,提出猜测:在点D运动的过程中,恒有CD=BE.经过与同学们的充分讨论,形成了几种证明的思路:
思路1:要证明CD=BE,只需要连接AE,并证明△ADC≌△AEB;
思路2:要证明CD=BE,只需要过点D作DF∥AB,交AC于F,证明△ADF≌△DEB;
思路3:要证明CD=BE,只需要延长CB至点G,使得BG=CD,证明△ADC≌△DEG;
…
请参考以上思路,帮助小玉证明CD=BE.(只需要用一种方法证明即可)
(3)小玉的发现启发了小明:如图3,若AB=AC=kBC,AD=kDE,且∠ADE=∠C,此时小明发现BE,BD,AC三者之间满足一定的数量关系,这个数量关系是 . (直接给出结论无须证明)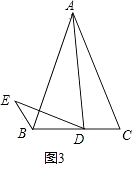
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E,∠ADC=70°.
(1)求∠EDC的度数;
(2)若∠ABC=n°,求∠BED的度数(用含n的代数式表示);
(3)将线段BC沿DC方向平移,使得点B在点A的右侧,其他条件不变,画出图形并判断∠BED的度数是否改变,若改变,求出它的度数(用含n的式子表示);若不改变,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com