
【题目】如图,四边形ABCD为平行四边形,∠BAD的角平分线AF交CD于点E,交BC的延长线于点F. 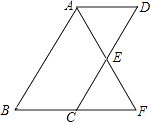
(1)求证:BF=CD;
(2)连接BE,若BE⊥AF,∠BFA=60°,BE=2 ![]() ,求平行四边形ABCD的周长.
,求平行四边形ABCD的周长. 
【答案】
(1)解:证明:∵四边形ABCD为平行四边形,
∴AB=CD,AD∥BC,
∴∠FAD=∠AFB,
又∵AF平分∠BAD,
∴∠FAD=∠FAB.
∴∠AFB=∠FAB.
∴AB=BF,
∴BF=CD
(2)解:∵由(1)知:AB=BF,
又∵∠BFA=60°,
∴△ABF为等边三角形,
∴AF=BF=AB,∠ABE=60°,
∵BE⊥AF,
∴点E是AF的中点.
∵在Rt△BEF中,∠BFA=60°,BE= ![]() ,
,
∴EF=2,BF=4,
∴AB=BF=4,
∵四边形BACD是平行四边形,
∴AB=CD,AD=BC,AB∥CD,
∴∠DCF=∠ABC=60°=∠F,
∴CE=EF,
∴△ECF是等边三角形,
∴CE=EF=CF=2,
∴BC=4﹣2=2,
∴平行四边形ABCD的周长为2+2+4+4=12
【解析】(1.)根据平行四边形的性质得出AB=CD,AD∥BC,求出∠FAD=∠AFB,根据角平分线定义得出∠FAD=∠FAB,求出∠AFB=∠FAB,即可得出答案; (2.)求出△ABF为等边三角形,根据等边三角形的性质得出AF=BF=AB,∠ABE=60°,在Rt△BEF中,∠BFA=60°,BE= ![]() ,解直角三角形求出EF=2,BF=4,AB=BF=4,BC=AD=2,即可得出答案.
,解直角三角形求出EF=2,BF=4,AB=BF=4,BC=AD=2,即可得出答案.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;
(2)AB=BC+AD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=mx2﹣4mx+2m﹣1(m≠0)与平行于x轴的一条直线交于A,B两点. 
(1)求抛物线的对称轴;
(2)如果点A的坐标是(﹣1,﹣2),求点B的坐标;
(3)抛物线的对称轴交直线AB于点C,如果直线AB与y轴交点的纵坐标为﹣1,且抛物线顶点D到点C的距离大于2,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=α,AC、BD交于M
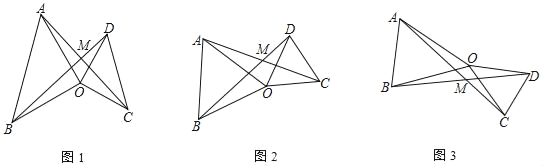
(1)如图1,当α=90°时,∠AMD的度数为 °
(2)如图2,当α=60°时,∠AMD的度数为 °
(3)如图3,当△OCD绕O点任意旋转时,∠AMD与α是否存在着确定的数量关系?如果存在,请你用表示∠AMD,并图3进行证明;若不确定,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由甲、乙两个工程队承包某校校园的绿化工程,甲、乙两队单独完成这项工作所需的时间比是3∶2,两队共同施工6天可以完成.
(1)求两队单独完成此项工程各需多少天?
(2)此项工程由甲、乙两队共同施工6天完成任务后,学校付给他们4000元报酬,若按各自完成的工程量分配这笔钱,问甲、乙两队各应得到多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图书管理员小张要骑车从学校到教育局,一出校门,遇到了王老师,王老师说:“今天有风,而且去时逆风,要吃亏了”,小张回答说:“去时逆风,回来时顺风,和无风往返一趟所用时间相同”.(顺风速度=无风时骑车速度+风速,逆风速度=无风时骑车速度-风速)
(1)如果学校到教育局的路程是15 km,无风时小张骑自行车的速度是20 km/h,他逆风去教育局所用时间是顺风回学校所用时间的![]() 倍,求风速是多少?
倍,求风速是多少?
(2)如果设从学校到教育局的路程为s千米,无风时骑车速度为v千米/时,风速为a千米/时(v>a),那么有风往返一趟的时间 无风往返一趟的时间(填“>”、“<”或“=”),试说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com