
【题目】由甲、乙两个工程队承包某校校园的绿化工程,甲、乙两队单独完成这项工作所需的时间比是3∶2,两队共同施工6天可以完成.
(1)求两队单独完成此项工程各需多少天?
(2)此项工程由甲、乙两队共同施工6天完成任务后,学校付给他们4000元报酬,若按各自完成的工程量分配这笔钱,问甲、乙两队各应得到多少元?
【答案】(1)甲队单独完成此项工程需要15天,乙队单独完成此项工程需要10天;(2)甲队应得的报酬为1600元,乙队应得的报酬为2400元.
【解析】
(1)设甲队单独完成此项工程需要3x天,则乙队单独完成此项工程需要2x天,根据两队共同施工6天可以完成该工程,即可得出关于x的分式方程,解之经检验即可得出结论;
(2)根据甲、乙两队单独完成这项工作所需的时间比可得出两队每日完成的工作量之比,再结合总报酬为4000元即可求出结论.
(1)设甲队单独完成此项工程需要3x天,则乙队单独完成此项工程需要2x天,
根据题意得:![]()
解得:x=5,
经检验,x=5是所列分式方程的解且符合题意.
∴3x=15,2x=10.
答:甲队单独完成此项工程需要15天,乙队单独完成此项工程需要10天.
(2)∵甲、乙两队单独完成这项工作所需的时间比是3:2,
∴甲、乙两队每日完成的工作量之比是2:3,
∴甲队应得的报酬为![]() (元),
(元),
乙队应得的报酬为4000﹣1600=2400(元).
答:甲队应得的报酬为1600元,乙队应得的报酬为2400元.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,AB,BC,CD分别与⊙O相切于E,F,G.且AB∥CD.BO=6cm,CO=8cm. 
(1)求证:BO⊥CO;
(2)求BE和CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABE=∠ACD=Rt∠,AE=AD,∠ABC=∠ACB.求证:∠BAE=∠CAD.

请补全证明过程,并在括号里写上理由.
证明:在△ABC中,
∵∠ABC=∠ACB
∴AB= ( )
在Rt△ABE和Rt△ACD中,
∵ =AC, =AD
∴Rt△ABE≌Rt△ACD( )
∴∠BAE=∠CAD( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题探究)
(1)如图①已知锐角△ABC,分别以AB、AC为腰,在△ABC的外部作等腰Rt△ABD和Rt△ACE,连接CD、BE,是猜想CD、BE的大小关系_____________ ;(不必证明)
(深入探究)
(2)如图②△ABC、△ADE都是等腰直角三角形,点D在边BC上(不与B、C重合),连接EC,则线段 BC,DC,EC 之间满足的等量关系式为________________ ;(不必证明) 线段 AD2,BD2,CD2之间满足的等量关系,并证明你的结论;
(拓展应用)
(3)如图③,在四边形 ABCD 中,∠ABC=∠ACB=∠ADC=45°.若 BD=9,CD=3,
求 AD 的长.

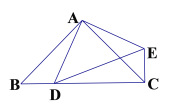

① ② ③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进某种茶壶、茶杯共200个进行销售,其中茶杯的数量是茶壶数量的5倍还多20个.销售方式有两种:(1)单个销售;(2)成套销售.相关信息如下表:
进价(元/个) | 单个售价(元/个) | 成套售价(元/套) | |
茶壶 | 24 | a | 55 |
茶杯 | 4 | a﹣30 | |
备注:(1)一个茶壶和和四个茶杯配成一套(如图); (2)利润=(售价﹣进价)×数量 | |||
(1)该商店购进茶壶和茶杯各有多少个?
(2)已知甲顾客花180元购买的茶壶数量与乙顾客花30元购买的茶杯数量相同.
①求表中a的值.
②当该商店还剩下20个茶壶和100个茶杯时,商店将这些茶壶和茶杯中的一部分按成套销售,其余按单个销售,这120个茶壶和茶杯全部售出后所得的利润为365元.问成套销售了多少套?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初中学生带手机上学,给学生带来了方便,同时也带来了一些负面影响.针对这种现象,某校九年级数学兴趣小组的同学随机调查了若干名家长对“初中学生带手机上学”现象的看法,统计整理并制作了如图的统计图: 
(1)这次调查的家长总人数为人,表示“无所谓”的家长人数为人;
(2)随机抽查一个接受调查的家长,恰好抽到“很赞同”的家长的概率是;
(3)求扇形统计图中表示“不赞同”的扇形的圆心角度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=2 ![]() ,∠C=120°,以点C为圆心的
,∠C=120°,以点C为圆心的 ![]() 与AB,AD分别相切于点G,H,与BC,CD分别相交于点E,F.若用扇形CEF作一个圆锥的侧面,则这个圆锥的高是 .
与AB,AD分别相切于点G,H,与BC,CD分别相交于点E,F.若用扇形CEF作一个圆锥的侧面,则这个圆锥的高是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC 中,AB=AC=6cm,∠B=∠C,BC=4cm,点 D 为 AB的中点.
(1)如果点 P 在线段 BC 上以 1cm/s 的速度由点 B 向点 C 运动,同时,点 Q 在线段 CA 上由点 C 向点 A 运动.
①若点 Q 的运动速度与点 P 的运动速度相等,经过 1 秒后,△BPD 与△CQP 是否全等,请说明理由;
②若点 Q 的运动速度与点 P 的运动速度不相等,当点 Q 的运动速度为多少时,能够使△BPD 与△CQP 全等?
(2)若点 Q 以②中的运动速度从点 C 出发,点 P 以原来的运动速度从点 B 同时出发,都逆时针沿△ABC 三边运动,则经过 后,点 P 与点 Q 第一次在△ABC 的 边上相遇?(在横线上直接写出答案,不必书写解题过程)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com