
����Ŀ������ѧ�����ֻ���ѧ����ѧ�������˷��㣬ͬʱҲ������һЩ����Ӱ�죮�����������ijУ���꼶��ѧ��ȤС���ͬѧ����������������ҳ��ԡ�����ѧ�����ֻ���ѧ������Ŀ�����ͳ����������������ͼ��ͳ��ͼ�� 
��1����ε���ļҳ�������Ϊ�ˣ���ʾ������ν���ļҳ�����Ϊ�ˣ�
��2��������һ�����ܵ���ļҳ���ǡ�ó鵽������ͬ���ļҳ��ĸ�������
��3��������ͳ��ͼ�б�ʾ������ͬ�������ε�Բ�ĽǶ�����
���𰸡�
��1��200��40
��2��![]()
��3���⣺������ͬ�������ε�Բ�ĽǶ���Ϊ�� ![]() ��360��=162�㣮
��360��=162�㣮
���������⣺��1.����ε���ļҳ�������Ϊ��50��25%=200���ˣ� ��ʾ������ν���ļҳ�����Ϊ��200��20%=40���ˣ�
���Դ��ǣ�200��40��
��2.��������ͬ���ļҳ�����Ϊ��200��90��50��40=20���ˣ�
�鵽������ͬ���ļҳ��ĸ�����20��200= ![]() ��
��
���Դ��ǣ� ![]() ��
��
�����㾫�����������⣬������Ҫ�˽�����ͳ��ͼ(������ر�ʾ������������������ռ�İٷֱȣ����Dz�������ر�ʾ��ÿ����Ŀ�ľ�����Ŀ�Լ�����ı仯���)����Ҫ��������ͳ��ͼ(������ر�ʾ��ÿ����Ŀ�ľ�����Ŀ�����Dz�������ر�ʾ��������������������ռ�İٷֱ��Լ�����ı仯���)�����֪ʶ���Ǵ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����P�ӵ�O����������ʱ�뷽�����ܳ�Ϊl��ͼ���˶�һ�ܣ�O��P�����ľ���y���P�߹���·��x�ĺ�����ϵ��ͼ����ô��P���ߵ�ͼ���ǣ� ��
A.
B.
C.
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������е��ĸ��������У�ͬһ�����������ͼ�븩��ͼ��ͬ���ǣ� ��
A.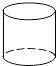
B.
C.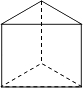
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ɼס����������̶ӳа�ijУУ���̻��������ס������ӵ����������������ʱ�����3��2�����ӹ�ͬʩ��6�������ɣ�
(1)�����ӵ�����ɴ���̸�������죿
(2)������ɼס������ӹ�ͬʩ��6������������ѧУ��������4000Ԫ����������������ɵĹ������������Ǯ���ʼס������Ӹ�Ӧ�õ�����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCΪ��O���ڽ������Σ�PΪBC�ӳ�����һ�㣬��PAC=��B��ADΪ��O��ֱ������C��CG��AD��AD��E����AB��F������O��G�� 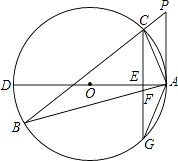
��1���ж�ֱ��PA���O��λ�ù�ϵ����˵�����ɣ�
��2����֤��AG2=AFAB��
��3������O��ֱ��Ϊ10��AC=2 ![]() ��AB=4
��AB=4 ![]() �����AFG�������
�����AFG�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�� ����ABCD�У�AB=8��BC=6��PΪAD��һ�㣬 ����ABP ��BP��������EBP�� PE��CD�ཻ�ڵ�O��BE��DC�ཻ��G�㣬��OE=OD��
��1����֤��AP=DG
��2������AP=x����GE=______��GC=_______���ú���x�Ĵ���ʽ��ʾ��������AP�ij���
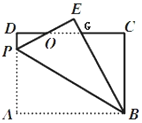
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1�����֣���ͼ1����AΪ�߶�BC��һ���㣬��BC=a��AB=b������Aλ��ʲô��ʱ���߶�AC�ij�ȡ�����ֵ�������ֵΪ���٣��ú�a��b��ʽ�ӱ�ʾ��
��2��Ӧ�ã���AΪ�߶�BC��һ���㣬��BC=4��AB=1����ͼ2��ʾ���ֱ���AB��ACΪ�ߣ����ȱ�������ABD�͵ȱ�������ACE������CD��BE��
�����ҳ�ͼ����BE��ȵ��߶Σ���˵�����ɣ�
��ֱ��д���߶�BE�������ֵ��
��3����չ����ͼ3����ƽ��ֱ������ϵ�У���A������Ϊ��2��0������B������Ϊ��6��0������PΪ�߶�AB��һ���㣬��PA=2��PM=PB����BPM=90�㣬��ֱ��д���߶�AM�������ֵ����ʱ��P�����꣮
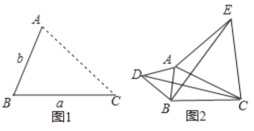
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����������ABC�У�BC>AB>AC���ס�����������һ��P��ʹ�á�BPC���A�������������ֱ����£�
���ף���AΪԲ�ģ�AC��Ϊ�뾶������AB��P�㣬��P��Ϊ����
���ң�����B������AB��ֱ��ֱ�ߣ�����C������AC��ֱ��ֱ�ߣ�����P�㣬��P��Ϊ����
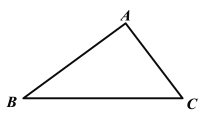
���ڼס������˵���������������������ȷ���� ���� ��
A. ���˽���ȷ
B. ���˽Դ���
C. ����ȷ���Ҵ���
D. �״�������ȷ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�ڼ��С����������ļ�ֵ�ۡ��ݽ������У�������ǰ20����ѡ�ֵ��ۺϷ���m���з���ͳ�ƣ���������ʾ��
��� | ���� | Ƶ�� |
һ | 6��m��7 | 2 |
�� | 7��m��8 | 7 |
�� | 8��m��9 | a |
�� | 9��m��10 | 2 |
��1����a��ֵ��
��2����������ͼ���������������8��m��9������Ӧ������ͼ��Բ�ĽǴ�С��
��3�����ڵ�һ���ڵ�����ѡ�ּ�Ϊ��A1��A2 �� �ڵ������ڵ�����ѡ�ּ�Ϊ��B1��B2 �� �ӵ�һ��͵����������ѡȡ2��ѡ�ֽ��е�����̸�����һ��������1��ѡ�ֱ�ѡ�еĸ��ʣ�����״ͼ���б����г����п��ܽ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com