
【题目】在下列的四个几何体中,同一几何体的主视图与俯视图相同的是( )
A.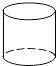
B.
C.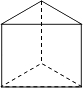
D.
科目:初中数学 来源: 题型:
【题目】如图,在等腰梯形ABCD中,AD∥BC,CA平分∠BCD,∠B=60°,若AD=3,则梯形ABCD的周长为( ) 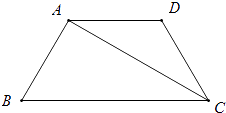
A.12 ![]()
B.15 ![]()
C.12
D.15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题情境】
课外兴趣小组活动时,老师提出了如下问题:
如图①,△ABC中,若AB=12,AC=8,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD至点E,使DE=AD,连接BE.请根据小明的方法思考:
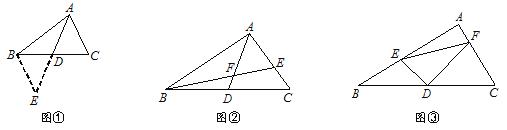
(1)由已知和作图能得到△ADC≌△EDB,依据是 .
A.SSS B.SAS C.AAS D.HL
(2)由“三角形的三边关系”可求得AD的取值范围是 .
解后反思:题目中出现“中点”、“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.
【初步运用】
如图②,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.若EF=3,EC=2,求线段BF的长.
【灵活运用】
如图③,在△ABC中, ∠A=90°,D为BC中点, DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.试猜想线段BE、CF、EF三者之间的等量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABE=∠ACD=Rt∠,AE=AD,∠ABC=∠ACB.求证:∠BAE=∠CAD.

请补全证明过程,并在括号里写上理由.
证明:在△ABC中,
∵∠ABC=∠ACB
∴AB= ( )
在Rt△ABE和Rt△ACD中,
∵ =AC, =AD
∴Rt△ABE≌Rt△ACD( )
∴∠BAE=∠CAD( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县为了了解初中生对安全知识掌握情况,抽取了50名初中生进行安全知识测试,并将测试成绩进行统计分析,绘制成了频数分布表和频数分布直方图(未完成). 安全知识测试成绩频数分布表
组别 | 成绩x(分数) | 组中值 | 频数(人数) |
1 | 90≤x<100 | 95 | 10 |
2 | 80≤x<90 | 85 | 25 |
3 | 70≤x<80 | 75 | 12 |
4 | 60≤x<70 | 65 | 3 |

(1)完成频数分布直方图;
(2)这个样本数据的中位数在第组;
(3)若将各组的组中值视为该组的平均成绩,则此次测试的平均成绩为;
(4)若将90分以上(含90分)定为“优秀”等级,则该县10000名初中生中,获“优秀”等级的学生约为人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题探究)
(1)如图①已知锐角△ABC,分别以AB、AC为腰,在△ABC的外部作等腰Rt△ABD和Rt△ACE,连接CD、BE,是猜想CD、BE的大小关系_____________ ;(不必证明)
(深入探究)
(2)如图②△ABC、△ADE都是等腰直角三角形,点D在边BC上(不与B、C重合),连接EC,则线段 BC,DC,EC 之间满足的等量关系式为________________ ;(不必证明) 线段 AD2,BD2,CD2之间满足的等量关系,并证明你的结论;
(拓展应用)
(3)如图③,在四边形 ABCD 中,∠ABC=∠ACB=∠ADC=45°.若 BD=9,CD=3,
求 AD 的长.

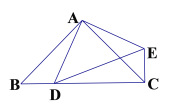

① ② ③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初中学生带手机上学,给学生带来了方便,同时也带来了一些负面影响.针对这种现象,某校九年级数学兴趣小组的同学随机调查了若干名家长对“初中学生带手机上学”现象的看法,统计整理并制作了如图的统计图: 
(1)这次调查的家长总人数为人,表示“无所谓”的家长人数为人;
(2)随机抽查一个接受调查的家长,恰好抽到“很赞同”的家长的概率是;
(3)求扇形统计图中表示“不赞同”的扇形的圆心角度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E是对角线AC上一点,且CE=CD,过点E作EF⊥AC交AD于点F,连接BE. 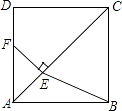
(1)求证:DF=AE;
(2)当AB=2时,求BE2的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com