
【题目】(问题探究)
(1)如图①已知锐角△ABC,分别以AB、AC为腰,在△ABC的外部作等腰Rt△ABD和Rt△ACE,连接CD、BE,是猜想CD、BE的大小关系_____________ ;(不必证明)
(深入探究)
(2)如图②△ABC、△ADE都是等腰直角三角形,点D在边BC上(不与B、C重合),连接EC,则线段 BC,DC,EC 之间满足的等量关系式为________________ ;(不必证明) 线段 AD2,BD2,CD2之间满足的等量关系,并证明你的结论;
(拓展应用)
(3)如图③,在四边形 ABCD 中,∠ABC=∠ACB=∠ADC=45°.若 BD=9,CD=3,
求 AD 的长.

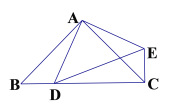

① ② ③
【答案】(1)CD=BE;(2)BC=CD+EC,BD2+CD2=2AD2,理由见解析;(3)AD =6.
【解析】
(1)如图所示,结论:CD = BE.只要证明△DAC≌△BAE即可;
(2)结论:BC=CD+EC, BD2+CD2=2AD2,依据△DAB≌△EAC可得BD=CE,AD=AE, ∠B=∠ACE=45°,因此CE +CD =AD +AE ,即可得出结论;
(3)作AE⊥AD,使AE=AD,连接CE,DE,证明△BAD≌△CAE,得到BD=CE=9,根据勾股定理计算算出DF=![]() ,从而得到AD=AF=6.
,从而得到AD=AF=6.
解:(1)CD=BE;
(2)BC=CD+EC,
BD2+CD2=2AD2,理由如下:
∵∠BAC=∠DAE=90°,
∴∠BAC-∠DAC=∠DAE-∠DAC,即∠BAD=∠CAE,
在△BAD和△CAE中,
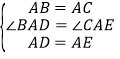 ,
,
∴△BAD≌△CAE,
∴BD=CE,∠ACE=∠B,
∴∠DCE=90°,
∴CE2+CD2=ED2,
在Rt△ADE中,AD2+AE2=ED2,又AD=AE,
∴BD2+CD2=2AD2;
(3)作AE⊥AD,使AE=AD,连接CE,DE,
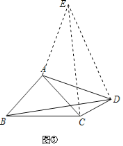
∵∠BAC+∠CAD=∠DAE+∠CAD,
即∠BAD=∠CAE,
在△BAD与△CAE中,
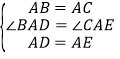 ,
,
∴△BAD≌△CAE(SAS),
∴BD=CE=9,
∵∠ADC=45°,∠EDA=45°,
∴∠EDC=90°,
∴DE=![]() =6
=6![]() ,
,
∵∠DAE=90°,
∴AD=AE=![]() DE=6.
DE=6.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】⊙O的半径为5,AB是⊙O的直径,点C在⊙O上,点D在直线AB上. 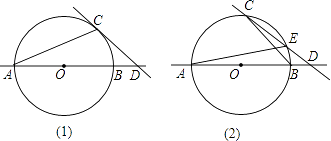
(1)如图(1),已知∠BCD=∠BAC,求证:CD是⊙O的切线;
(2)如图(2),CD与⊙O交于另一点E.BD:DE:EC=2:3:5,求圆心O到直线CD的距离;
(3)若图(2)中的点D是直线AB上的动点,点D在运动过程中,会出现C,D,E在三点中,其中一点是另外两点连线的中点的情形,问这样的情况出现几次?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=21,BC=13,D是AC边上一点,BD=12,AD=16,
(1)若E是边AB的中点,求线段DE的长
(2)若E是边AB上的动点,求线段DE的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由甲、乙两个工程队承包某校校园的绿化工程,甲、乙两队单独完成这项工作所需的时间比是3∶2,两队共同施工6天可以完成.
(1)求两队单独完成此项工程各需多少天?
(2)此项工程由甲、乙两队共同施工6天完成任务后,学校付给他们4000元报酬,若按各自完成的工程量分配这笔钱,问甲、乙两队各应得到多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为⊙O的内接三角形,P为BC延长线上一点,∠PAC=∠B,AD为⊙O的直径,过C作CG⊥AD交AD于E,交AB于F,交⊙O于G. 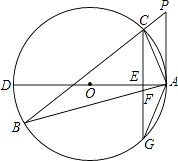
(1)判断直线PA与⊙O的位置关系,并说明理由;
(2)求证:AG2=AFAB;
(3)若⊙O的直径为10,AC=2 ![]() ,AB=4
,AB=4 ![]() ,求△AFG的面积.
,求△AFG的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
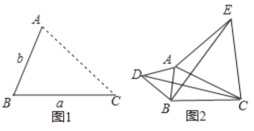
【题目】(1)发现:如图1,点A为线段BC外一动点,且BC=a,AB=b.当点A位于什么上时,线段AC的长取得最大值,且最大值为多少(用含a,b的式子表示)
(2)应用:点A为线段BC外一动点,且BC=4,AB=1,如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE.
①请找出图中与BE相等的线段,并说明理由;
②直接写出线段BE长的最大值.
(3)拓展:如图3,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(6,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,请直接写出线段AM长的最大值及此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com