
【题目】⊙O的半径为5,AB是⊙O的直径,点C在⊙O上,点D在直线AB上. 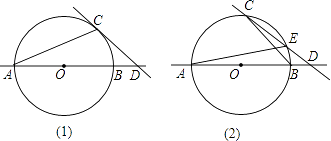
(1)如图(1),已知∠BCD=∠BAC,求证:CD是⊙O的切线;
(2)如图(2),CD与⊙O交于另一点E.BD:DE:EC=2:3:5,求圆心O到直线CD的距离;
(3)若图(2)中的点D是直线AB上的动点,点D在运动过程中,会出现C,D,E在三点中,其中一点是另外两点连线的中点的情形,问这样的情况出现几次?
【答案】
(1)证明:如图(1),连接OC,
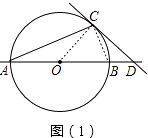
∵OA=OC,
∴∠OAC=∠OCA,
又∵AB是⊙O的直径,
∴∠ACB=90°,
又∵∠BCD=∠BAC=∠OCA,
∴∠BCD+∠OCB=90°,即OC⊥CD,
∴CD是⊙O的切线
(2)解:∵∠ADE=∠CDB,∠BCD=∠EAD,
∴△BCD∽△EAD,
∴ ![]() ,
,
∴ ![]() ,
,
又∵BD:DE:EC=2:3:5,⊙O的半径为5,
∴BD=2,DE=3,EC=5,
如图(2),连接OC、OE,则△OEC是等边三角形,
作OF⊥CE于F,则EF= ![]() CE=
CE= ![]() ,∴OF=
,∴OF= ![]() ,
,
∴圆心O到直线CD的距离是 ![]() .
.
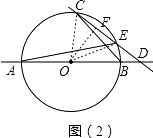
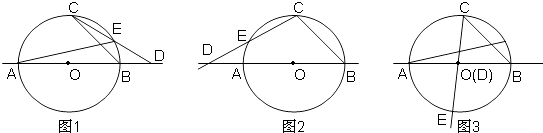
(3)解:这样的情形共有出现三次:
当点D在⊙O外时,点E是CD中点,有以下两种情形,如图1、图2;
当点D在⊙O内时,点D是CE中点,有以下一种情形,如图3.
【解析】(1)连接OC,根据弦切角定理和圆的性质可得到∠BCD=∠BAC=∠OCA,结合圆周角定理可求得∠OCD=90°,可证明CD是切线;(2)先证明△BCD∽△EAD,结合条件可求得BD=2,DE=3,EC=5,在△OBC中可求得O到CD的距离;(3)分点D在⊙O外和点D在⊙O内两种情况,当D在⊙O外时又分D在A点左边和D在B点右边两种情况,当D在⊙O内时只有一种,结合图形可给出答案.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:初中数学 来源: 题型:
【题目】规定两数a、b之间的一种运算,记作(a,b):如果![]() ,那么(a,b)=c.
,那么(a,b)=c.
例如:因为![]() ,所以(2,8)=3.
,所以(2,8)=3.
(1)根据上述规定,填空:
(5,125)= ,(-2,4)= ,(-2,-8)= ;
(2)小明在研究这种运算时发现一个现象:![]() ,他给出了如下的证明:
,他给出了如下的证明:
设![]() ,则
,则![]() ,即
,即![]()
∴![]() ,即
,即![]() ,
,
∴![]() .
.
请你尝试运用上述这种方法说明下面这个等式成立的理由.
(4,5)+(4,6)=(4,30)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘海轮在A点时测得灯塔C在它的北偏东42°方向上,它沿正东方向航行80海里后到达B处,此时灯塔C在它的北偏西55°方向上.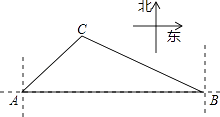
(1)求海轮在航行过程中与灯塔C的最短距离(结果精确到0.1);
(2)求海轮在B处时与灯塔C的距离(结果保留整数).
(参考数据:sin55°≈0.819,cos55°≈0.574,tan55°≈1.428,tan42°≈0.900,tan35°≈0.700,tan48°≈1.111)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题情境】
课外兴趣小组活动时,老师提出了如下问题:
如图①,△ABC中,若AB=12,AC=8,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD至点E,使DE=AD,连接BE.请根据小明的方法思考:
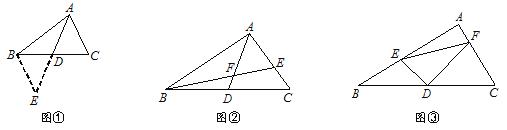
(1)由已知和作图能得到△ADC≌△EDB,依据是 .
A.SSS B.SAS C.AAS D.HL
(2)由“三角形的三边关系”可求得AD的取值范围是 .
解后反思:题目中出现“中点”、“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.
【初步运用】
如图②,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.若EF=3,EC=2,求线段BF的长.
【灵活运用】
如图③,在△ABC中, ∠A=90°,D为BC中点, DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.试猜想线段BE、CF、EF三者之间的等量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班毕业联欢会设计的即兴表演节目的摸球游戏,游戏采用一个不透明的盒子,里面装有五个分别标有数字1、2、3、4、5的乒乓球,这些球除数字外,其它完全相同,游戏规则是参加联欢会的50名同学,每人将盒子乒乓球摇匀后闭上眼睛从中随机一次摸出两个球(每位同学必须且只能摸一次).若两球上的数字之和是偶数就给大家即兴表演一个节目;否则,下个同学接着做摸球游戏,依次进行.
(1)用列表法或画树状图法求参加联欢会同学表演即兴节目的概率;
(2)估计本次联欢会上有多少个同学表演即兴节目.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABE=∠ACD=Rt∠,AE=AD,∠ABC=∠ACB.求证:∠BAE=∠CAD.

请补全证明过程,并在括号里写上理由.
证明:在△ABC中,
∵∠ABC=∠ACB
∴AB= ( )
在Rt△ABE和Rt△ACD中,
∵ =AC, =AD
∴Rt△ABE≌Rt△ACD( )
∴∠BAE=∠CAD( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县为了了解初中生对安全知识掌握情况,抽取了50名初中生进行安全知识测试,并将测试成绩进行统计分析,绘制成了频数分布表和频数分布直方图(未完成). 安全知识测试成绩频数分布表
组别 | 成绩x(分数) | 组中值 | 频数(人数) |
1 | 90≤x<100 | 95 | 10 |
2 | 80≤x<90 | 85 | 25 |
3 | 70≤x<80 | 75 | 12 |
4 | 60≤x<70 | 65 | 3 |

(1)完成频数分布直方图;
(2)这个样本数据的中位数在第组;
(3)若将各组的组中值视为该组的平均成绩,则此次测试的平均成绩为;
(4)若将90分以上(含90分)定为“优秀”等级,则该县10000名初中生中,获“优秀”等级的学生约为人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题探究)
(1)如图①已知锐角△ABC,分别以AB、AC为腰,在△ABC的外部作等腰Rt△ABD和Rt△ACE,连接CD、BE,是猜想CD、BE的大小关系_____________ ;(不必证明)
(深入探究)
(2)如图②△ABC、△ADE都是等腰直角三角形,点D在边BC上(不与B、C重合),连接EC,则线段 BC,DC,EC 之间满足的等量关系式为________________ ;(不必证明) 线段 AD2,BD2,CD2之间满足的等量关系,并证明你的结论;
(拓展应用)
(3)如图③,在四边形 ABCD 中,∠ABC=∠ACB=∠ADC=45°.若 BD=9,CD=3,
求 AD 的长.

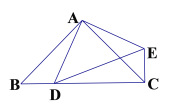

① ② ③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校举行“社会主义核心价值观”知识比赛活动,全体学生都参加比赛,学校对参赛学生均给与表彰,并设置一、二、三等奖和纪念奖共四个奖项,赛后将获奖情况绘制成如下所示的两幅不完整的统计图,请根据图中所给的信息,解答下列问题: 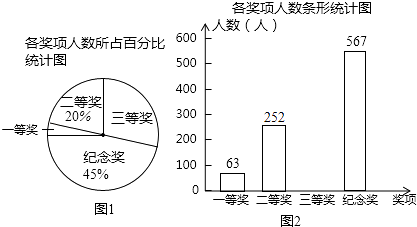
(1)该校共有名学生;
(2)在图①中,“三等奖”所对应扇形的圆心角度数是;
(3)将图②补充完整;
(4)从该校参加本次比赛活动的学生中随机抽查一名.求抽到获得一等奖的学生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com