Question

【题目】如图，在等腰梯形ABCD中，AD∥BC，CA平分∠BCD，∠B=60°，若AD=3，则梯形ABCD的周长为（ ）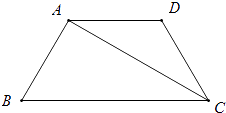
A.12
B.15
C.12
D.15

Answer 1

【答案】D
【解析】解：过点A作AE∥CD，交BC于点E， ∵梯形ABCD是等腰梯形，∠B=60°，
∴AD∥BC，
∴四边形ADCE是平行四边形，
∴∠AEB=∠BCD=60°，
∵CA平分∠BCD，
∴∠ACE= ∠BCD=30°，
∵∠AEB是△ACE的外角，
∴∠AEB=∠ACE+∠EAC，即60°=30°+∠EAC，
∴∠EAC=30°，
∴AE=CE=3，
∴四边形ADEC是菱形，
∵△ABE中，∠B=∠AEB=60°，
∴△ABE是等边三角形，
∴AB=BE=AE=3，
∴梯形ABCD的周长=AB+（BE+CE）+CD+AD=3+3+3+3+3=15．
故选：D．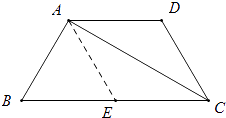

【考点精析】解答此题的关键在于理解等腰梯形的性质的相关知识，掌握等腰梯形的两腰相等；同一底上的两个角相等；两条对角线相等．