
【题目】如图,直线y=﹣2x+4与坐标轴分别交于C、B两点,过点C作CD⊥x轴,点P是x轴下方直线CD上的一点,且△OCP与△OBC相似,求过点P的双曲线解析式.
【答案】解:∵直线y=﹣2x+4与坐标轴分别交于C、B两点,
∴令y=0,可得﹣2x+4=0,解得x=2,即C(2,0),OC=2,
令x=0,可得y=4,即B(0,4),OB=4,
①如图1,当∠OBC=∠COP时,△OCP∽△BOC,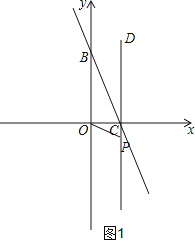
∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得CP=1,
,解得CP=1,
∴P(2,﹣1),
设过点P的双曲线解析式y=![]() ,把P点代入解得k=﹣2,
,把P点代入解得k=﹣2,
∴过点P的双曲线解析式y=﹣![]() ,
,
②如图2,当∠OBC=∠CPO时,△OCP∽△COB,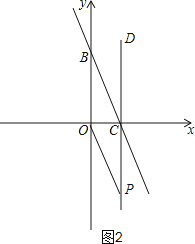
在△OCP和△COB中,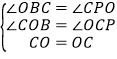
∴△OCP≌△COB(AAS)
∴CP=BO=4,
∴P(2,﹣4)
设过点P的双曲线解析式y=![]() ,把P点代入得﹣4=
,把P点代入得﹣4=![]() ,解得k=﹣8,
,解得k=﹣8,
∴过点P的双曲线解析式y=![]() .
.
综上可得,过点P的双曲线的解析式为y=﹣![]() 或y=
或y=![]() .
.
【解析】由直线y=﹣2x+4与坐标轴分别交于C、B两点,易得OC=2,OB=4,再分两种情况①当∠OBC=∠COP时,△OCP与△OBC相似,②当∠OBC=∠CPO时,△OCP与△OBC相似分别求出点的坐标,再求出过点P的双曲线解析式.
【考点精析】解答此题的关键在于理解相似三角形的判定与性质的相关知识,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是一片水田,某村民小组需计算其面积,测得如下数据:
∠A=90°,∠ABD=60°,∠CBD=54°,AB=200m,BC=300m.
请你计算出这片水田的面积.
(参考数据:sin54°≈0.809,cos54°≈0.588,tan54°≈1.376, ![]() ≈1.732)
≈1.732)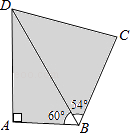
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某市2016年四月每日的最低气温(℃)的统计图,则在四月份每日的最低气温这组数据中,中位数和众数分别是( ) 
A.14℃,14℃
B.15℃,15℃
C.14℃,15℃
D.15℃,14℃
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一架云梯AB的长25 m,斜靠在一面墙上,梯子靠墙的一端A距地面距离AC为24 m.
(1)这个梯子底端B离墙的距离BC有多少米?
(2)如果梯子的顶端下滑了4 m,那么梯子的底部在水平方向也滑动了4 m吗?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定两数a、b之间的一种运算,记作(a,b):如果![]() ,那么(a,b)=c.
,那么(a,b)=c.
例如:因为![]() ,所以(2,8)=3.
,所以(2,8)=3.
(1)根据上述规定,填空:
(5,125)= ,(-2,4)= ,(-2,-8)= ;
(2)小明在研究这种运算时发现一个现象:![]() ,他给出了如下的证明:
,他给出了如下的证明:
设![]() ,则
,则![]() ,即
,即![]()
∴![]() ,即
,即![]() ,
,
∴![]() .
.
请你尝试运用上述这种方法说明下面这个等式成立的理由.
(4,5)+(4,6)=(4,30)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=13,AC=5,BC边上的中线AD=6,点E在AD的延长线上,且AD=DE.
(1)试判断△ABE的形状并说明理由;
(2)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰梯形ABCD中,AD∥BC,CA平分∠BCD,∠B=60°,若AD=3,则梯形ABCD的周长为( ) 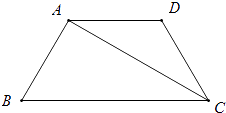
A.12 ![]()
B.15 ![]()
C.12
D.15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB,BC,CD分别与⊙O相切于E,F,G.且AB∥CD.BO=6cm,CO=8cm. 
(1)求证:BO⊥CO;
(2)求BE和CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABE=∠ACD=Rt∠,AE=AD,∠ABC=∠ACB.求证:∠BAE=∠CAD.

请补全证明过程,并在括号里写上理由.
证明:在△ABC中,
∵∠ABC=∠ACB
∴AB= ( )
在Rt△ABE和Rt△ACD中,
∵ =AC, =AD
∴Rt△ABE≌Rt△ACD( )
∴∠BAE=∠CAD( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com