【题目】在△ABC中，AB=13，AC=5，BC边上的中线AD=6，点E在AD的延长线上，且AD=DE．
（1）试判断△ABE的形状并说明理由；
（2）求△ABC的面积．
【答案】（1）△ABE是直角三角形；证明见解析；（2）30
【解析】
（1）证明△ACD≌△EBD，得到BE=AC=5，再由AE=12，AB=13，得到∠E=90°，从而得到结论；
（2）由△ACD≌△EBD ，得到S△ABC=S△ABE，从而得到结论．
（1）∵AD为BC边上的中线，∴BD=CD．
在△ACD与△EBD中，∵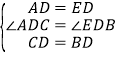
，∴△ACD≌△EBD，∴BE=AC=5．
∵AD=DE=6，∴AE=12．
∵AE2+BE2=52+122=169，AB2=132=169，∴AE2+BE2= AB2，∴∠E=90°，∴△ABE是直角三角形．
（2）∵△ACD≌△EBD ，∴S△ABC=S△ABE=
×EA×BE=×12×5 =30．
课堂全解字词句段篇章系列答案科目：初中数学 来源： 题型：
【题目】尺规作图：某学校正在进行校园环境的改造工程设计，准备在校内一块四边形花坛内栽上一棵桂花树．如图，要求桂花树的位置（视为点P），到花坛的两边AB、BC的距离相等，并且点P到点A、D的距离也相等．请用尺规作图作出栽种桂花树的位置点P（不写作法，保留作图痕迹）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，∠C=Rt∠，AB=5cm，BC=3cm，若动点P从点C开始，按C→A→B→C的路径运动，且速度为每秒1cm，设出发的时间为t秒．
（1）出发2秒后，求△ABP的周长．
（2）问t满足什么条件时，△BCP为直角三角形？
（3）另有一点Q，从点C开始，按C→B→A→C的路径运动，且速度为每秒2cm，若P、Q两点同时出发，当P、Q中有一点到达终点时，另一点也停止运动．当t为何值时，直线PQ把△ABC的周长分成相等的两部分？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在Rt△ABC中，∠ACB=
，D是AB边上的一点，过D作DE⊥AB交AC于点E，BC=BD，连结CD交BE于点F.
（1）求证：CE=DE；
（2）若点D为AB的中点，求∠AED的度数.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线y=﹣2x+4与坐标轴分别交于C、B两点，过点C作CD⊥x轴，点P是x轴下方直线CD上的一点，且△OCP与△OBC相似，求过点P的双曲线解析式．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，A（-1，0），B（1，0），C（0，1），点D为x轴正半轴上的一个动点，点E为第一象限内一点，且CE⊥CD，CE=CD．
（1）试说明：∠EBC＝∠CAB ；
（2）取DE的中点F，连接OF，试判断OF与AC的位置关系，并说明理由；
（3）在（2）的条件下，试探索O、D、F三点能否构成等腰三角形，若能，请直接写出所有符合条件的点D的坐标；若不能，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】以下列数组作为三角形的三条边长，其中能构成直角三角形的是( )
A. 1， 
，3 B. 
， 
，5 C. 1.5，2，2.5 D. 
， 
， 
【答案】C
【解析】A、12+（
）2≠32，不能构成直角三角形，故选项错误；
B、(
2+（
）2≠52，不能构成直角三角形，故选项错误；
C、1.52+22=2.52，能构成直角三角形，故选项正确；
D、（
））2+（
）2≠（
）2，不能构成直角三角形，故选项错误．
故选：C．
【题型】单选题
【结束】
3
【题目】在Rt△ABC中，∠C=90°，AC=9，BC=12，则点C到斜边AB的距离是（ ）
（A）
（B）
（C）9 （D）6
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC是等边三角形，D是BC的中点．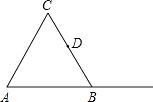 
（1）作图： ①过B作AC的平行线BH；
②过D作BH的垂线，分别交AC，BH，AB的延长线于E，F，G．
（2）在图中找出一对全等的三角形，并证明你的结论．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
