
����Ŀ����ƽ��ֱ������ϵxOy�У�A��-1��0����B��1��0����C��0��1������DΪx���������ϵ�һ�����㣬��EΪ��һ������һ�㣬��CE��CD��CE=CD��
��1����˵������EBC����CAB ��
��2��ȡDE���е�F������OF�����ж�OF��AC��λ�ù�ϵ����˵�����ɣ�
��3���ڣ�2���������£���̽��O��D��F�����ܷɵ��������Σ����ܣ���ֱ��д�����з��������ĵ�D�����ꣻ�����ܣ���˵�����ɣ�

���𰸡���1��֤������������2��OF��AC����3��D(1��0)��D��1+![]() ��0��
��0��
��������
��1����֤��AOC����BOC��Ϊ����ֱ�������Σ��ҡ�ACD=��ECB���Ӷ��õ�
��ACD�ա�BCE����ȫ�������ζ�Ӧ����ȼ��ɵó����ۣ�
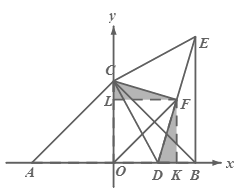
��2����FL��OC ��FK��OB����֤��CFL=��KFD��CF=DF=![]() DE���õ���CFL�ա�DFK����ȫ�������ζ�Ӧ����ȵõ�FL=FK���ɽ�ƽ�����ж������õ�OFƽ�֡�COB���Ӷ��õ���COF=��BOF=45�㣬���ɵõ�OF��AC��
DE���õ���CFL�ա�DFK����ȫ�������ζ�Ӧ����ȵõ�FL=FK���ɽ�ƽ�����ж������õ�OFƽ�֡�COB���Ӷ��õ���COF=��BOF=45�㣬���ɵõ�OF��AC��
��3����D��x��0��(x��0)����OD=x����E��EG��y����G�����EGC�ա�COD���õ�E�����������е����깫ʽ�õ�F�����������������빫ʽ�õ�OF��DF�ij���Ȼ������������������OD=OF����OD=FD����OF=FD��
��1����A��-1��0����B��1��0����C��0��1������AO=CO=BO=1��
��CO��AB����AC=BC����AOC����BOC��Ϊ����ֱ�������Σ����CBO=��BCO=��ACO=��CAO =45������ACB=90��������ACD+��BCD =90����
�֡�CE��CD�����ECB+��BCD =90�������ACD=��ECB��
�ڡ�ACD���BCE�У���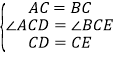 �����ACD�ա�BCE�����EBC����CAB��
�����ACD�ա�BCE�����EBC����CAB��
��2��OF��AC���������£�
��FL��OC ��FK��OB����ͼ����CO��BO�����LFK =90����
��CE=CD����F��DE���е㣬��CF��DE�����CFL+��LFD =90�㣮
�֡ߡ�KFD+��LFD =90�������CFL=��KFD��
��CE��CD����F��DE���е㣬��CF=DF=![]() DE��
DE��
�ڡ�CFL���DFK�У���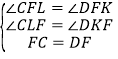 �����CFL�ա�DFK����FL=FK��
�����CFL�ա�DFK����FL=FK��
�֡�FL��OC ��FK��OB����OFƽ�֡�COB�����COF=��BOF=45�㣮
�֡ߡ�CAO =45������BOF=��CAO����OF��AC��
��3����D��x��0��(x��0)����OD=x����E��EG��y����G��
��CE��CD�����ECD=90�㣬���GCE+��DCO=90�㣮
�ߡ�GCE+��GEC=90�㣬���GEC=��OCD��
�ߡ�EGC=��COD=90�㣬CE=CD�����EGC�ա�COD����GE=OC=1��CG=OD=x����E��1��x+1����
��FΪED���е�����F(![]() ��
��![]() )����OF=
)����OF=![]() =
=![]() ��DF=
��DF=![]() =
=![]() ��
��
��ODF���������������������������
��OD=OF����x=![]() �������x=
�������x=![]() ����D(
����D(![]() ��0)��
��0)��
��OD=FD����x=![]() �������x=��1��������ȥ������x=1����D(1��0)��
�������x=��1��������ȥ������x=1����D(1��0)��
��OF=FD����![]() =
=![]() �������x=0(��ȥ)������������������
�������x=0(��ȥ)������������������
����������D(1��0)��D(![]() ��0)��
��0)��


 �㽭��У��ʦ���ϵ�д�
�㽭��У��ʦ���ϵ�д� ȫ�ų��100��ϵ�д�
ȫ�ų��100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ����ǧ�ܣ���ͼ�Ǵ����濴������ǧ������Ȼ�´�ʱ��̤�������0.5m��̤���Ⱥ��Բ��ƣ��� ��ͼ�ǴӲ��濴������ǧ̤�嵴������Bλ��ʱ����B����洹ֱ�߶�BCΪ1m������ǧ֧��AD��ˮƽ����BEΪ1.5m��������֧����ֱ����.����ǧ֧��AD�ĸ�.


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
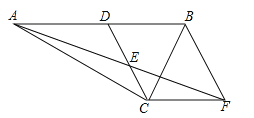
����Ŀ����֪����ͼ����Rt��ACB�У���ACB=90�㣬��D��AB���е㣬��E��CD���е㣬����C��CF��AB��AE���ӳ����ڵ�F��
��1����֤����ADE�ա�FCE��
��2������DCF=120�㣬DE=2����BC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ����ѧ���ֻ�������Խ��Խ�ܵ����Ĺ�ע��Ϊ��ý��������������ijУ������ѧ����ѧ���ֻ���Ŀ�ģ���Ϊ�������ͣ�A�����绰��B�շ����ţ�C�������ϣ�D��Ϸ���죮�������������Ƴ�ͼ1��ͼ2��ͳ��ͼ�����������������ͼ���ṩ����Ϣ������������⣺
��1���˴γ��������У��������� ��ѧ��.
��2����ͼ1��ͼ2����������
��3������4��ѧ��������A��������B��������������ѡ2��ѧ������������ѧ��Ϊͬһ���͵ĸ��ʣ����б�������״ͼ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У�AB=13��AC=5��BC���ϵ�����AD=6����E��AD���ӳ����ϣ���AD=DE��
��1�����жϡ�ABE����״��˵�����ɣ�
��2�����ABC�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ż���һ����ѧ��У����á������һ���ľ����У������ε��ܳ���̡��Ľ��ۣ��Ƶ�����ʽ��x+ ![]() ��x��0������Сֵ��2�������Ƶ��������£��������1�ľ���������ε�һ�߳�Ϊx������һ�߳���
��x��0������Сֵ��2�������Ƶ��������£��������1�ľ���������ε�һ�߳�Ϊx������һ�߳��� ![]() �����ε��ܳ���2��x+
�����ε��ܳ���2��x+ ![]() ���������γ�Ϊ������ʱ������x=
���������γ�Ϊ������ʱ������x= ![]() ��x��0�������x=1����ʱ���ε��ܳ�2��x+
��x��0�������x=1����ʱ���ε��ܳ�2��x+ ![]() ��=4��С�����x+
��=4��С�����x+ ![]() ��x��0������Сֵ��2��ģ���Ż����Ƶ��������ʽ��
��x��0������Сֵ��2��ģ���Ż����Ƶ��������ʽ�� ![]() ��x��0������Сֵ�ǣ� ��
��x��0������Сֵ�ǣ� ��
A.2
B.1
C.6
D.10
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧϰ��Ϊ�ִ��˵�ʱ�У�ij���йز���ͳ�������6���µ�ͼ��ݵĶ��ߵ�ְҵ�ֲ����������������������������ͳ��ͼ�� 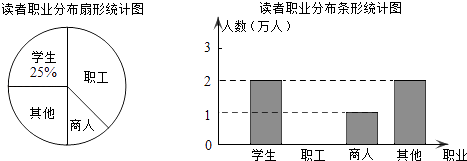
��1����ͳ�Ƶ����ʱ���ڣ��������˴ε�ͼ����Ķ�����������ռ�ٷֱ�Ϊ%��
��2��������ͳ��ͼ����������
��3����5�·ݵ�ͼ��ݵĶ��߹�28000�˴Σ���������Լ�ж����˴ζ�����ְ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���ͼ��Ķ�����ԭ��O��������A��1�� ![]() ������F��0��1����y���ϣ�ֱ��y=��1��y�ύ�ڵ�H��
������F��0��1����y���ϣ�ֱ��y=��1��y�ύ�ڵ�H��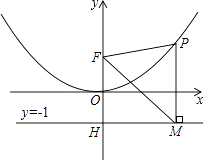
��1������κ����Ľ���ʽ��
��2����P�ǣ�1����ͼ���ϵĵ㣬����P��x��Ĵ�����ֱ��y=��1���ڵ�M����֤��FMƽ�֡�OFP��
��3������FPM�ǵȱ�������ʱ����P������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��1������ƽ��ֱ������ϵxOy�У�������y=ax2+bx+c��a��0����x�ύ��A����1��0����B��3��0������y�ύ��C��0��3��������ΪD��1��4�����Գ���ΪDE��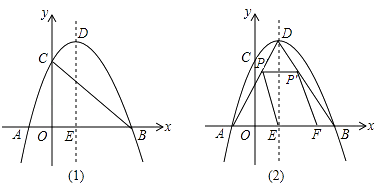
��1�������ߵĽ���ʽ����
��2����ͼ��2������P��AD��һ�����㣬P����P����DE�ĶԳƵ㣬����PE����P����P��F��PE��x����F����S�ı���EPP��F=y��EF=x����y����x�ĺ�����ϵʽ������y�����ֵ��
��3���ڣ�1���е����������Ƿ���ڵ�Q��ʹ��BCQ��Ϊ��BCΪֱ�DZߵ�ֱ�������Σ������ڣ����Q�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com