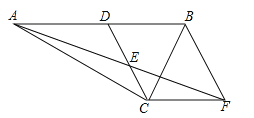
【题目】已知：如图，在Rt△ACB中，∠ACB=90°，点D是AB的中点，点E是CD的中点，过点C作CF∥AB叫AE的延长线于点F．
（1）求证：△ADE≌△FCE；
（2）若∠DCF=120°，DE=2，求BC的长．
【答案】（1）证明见解析；（2）4．
【解析】试题分析：（1）先根据点E是CD的中点得出DE=CE，再由AB∥CF可知∠BAF=∠AFC，根据AAS定理可得出△ADE≌△FCE；
（2）根据直角三角形的性质可得出AD=CD=
AB，再由AB∥CF可知∠BDC=180°﹣∠DCF=180°﹣120°=60°，由三角形外角的性质可得出∠DAC=∠ACD=∠BDC=30°，进而可得出结论．
试题解析：（1）证明：∵点E是CD的中点，∴DE=CE．
∵AB∥CF，∴∠BAF=∠AFC．
在△ADE与△FCE中，∵∠BAF=∠AFC，∠AED=∠FEC，DE=CE，∴△ADE≌△FCE（AAS）；
（2）解：由（1）得，CD=2DE，∵DE=2，∴CD=4．
∵点D为AB的中点，∠ACB=90°，∴AB=2CD=8，AD=CD=AB．
∵AB∥CF，∴∠BDC=180°﹣∠DCF=180°﹣120°=60°，∴∠DAC=∠ACD=∠BDC=×60°=30°，∴BC=AB=×8=4．
习题精选系列答案科目：初中数学 来源： 题型：
【题目】蔬菜经营户老王，近两天经营的是青菜和西兰花．
（1）昨天的青菜和西兰花的进价和售价如表，老王用600元批发青菜和西兰花共200市斤，当天售完后老王一共能赚多少元钱？
青菜 | 西兰花 | |
进价（元/市斤） | 2.8 | 3.2 |
售价（元/市斤） | 4 | 4.5 |
（2）今天因进价不变，老王仍用600元批发青菜和西兰花共200市斤．但在运输中青菜损坏了10%，而西兰花没有损坏仍按昨天的售价销售，要想当天售完后所赚的钱不少于昨天所赚的钱，请你帮老王计算，应怎样给青菜定售价？（精确到0.1元）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知△EFG≌△NMH, ∠F与∠M是对应角．
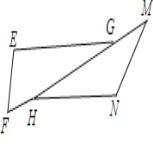
（1）写出相等的线段与相等的角；
（2）若EF=2.1cm，FH=1.1cm，HM=3.3cm，求MN和HG的长度.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，∠C=Rt∠，AB=5cm，BC=3cm，若动点P从点C开始，按C→A→B→C的路径运动，且速度为每秒1cm，设出发的时间为t秒．
（1）出发2秒后，求△ABP的周长．
（2）问t满足什么条件时，△BCP为直角三角形？
（3）另有一点Q，从点C开始，按C→B→A→C的路径运动，且速度为每秒2cm，若P、Q两点同时出发，当P、Q中有一点到达终点时，另一点也停止运动．当t为何值时，直线PQ把△ABC的周长分成相等的两部分？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正方形网格中的每个小正方形边长都是1．请同学们利用网格线进行画图：
(1)在图1中，画一个顶点为格点、面积为5的正方形；
(2)在图2中，已知线段AB、CD，画线段EF，使它与AB、CD组成轴对称图形；(要求画出所有符合题意的线段)
(3)在图3中，找一格点D，满足：①到CB、CA的距离相等；②到点A、C的距离相等．
查看答案和解析>>
科目：初中数学 来源： 题型：
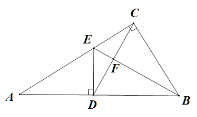
【题目】如图，在Rt△ABC中，∠ACB=
，D是AB边上的一点，过D作DE⊥AB交AC于点E，BC=BD，连结CD交BE于点F.
（1）求证：CE=DE；
（2）若点D为AB的中点，求∠AED的度数.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，A（-1，0），B（1，0），C（0，1），点D为x轴正半轴上的一个动点，点E为第一象限内一点，且CE⊥CD，CE=CD．
（1）试说明：∠EBC＝∠CAB ；
（2）取DE的中点F，连接OF，试判断OF与AC的位置关系，并说明理由；
（3）在（2）的条件下，试探索O、D、F三点能否构成等腰三角形，若能，请直接写出所有符合条件的点D的坐标；若不能，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC是等边三角形，D是BC的中点．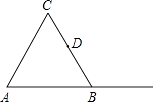 
（1）作图： ①过B作AC的平行线BH；
②过D作BH的垂线，分别交AC，BH，AB的延长线于E，F，G．
（2）在图中找出一对全等的三角形，并证明你的结论．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
