
【题目】如图,△ABC中,∠C=Rt∠,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.

(1)出发2秒后,求△ABP的周长.
(2)问t满足什么条件时,△BCP为直角三角形?
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?
【答案】(1))△ABP的周长(7+![]() )cm;(2)
)cm;(2)![]() 或
或![]() 时,△BCP为直角三角形;(3)t=2或6.
时,△BCP为直角三角形;(3)t=2或6.
【解析】试题分析:(1)过P作PE⊥AB,设CP=2t,根据角平分线的性质和勾股定理进行解答即可;
(2)分类讨论:当CP=CB时,△BCP为等腰三角形,若点P在AC上得t=3(s),若点P在AB上,则t=5.4s;当PC=PB时,△BCP为等腰三角形,作PD⊥BC于D,根据等腰三角形的性质得BD=CD,则可判断PD为△ABC的中位线,则AP=![]() AB=
AB=![]() ,易得t=
,易得t=![]() (s);当BP=BC=3时,△BCP为等腰三角形,则AP=AB-BP=2,易得t=6(s);
(s);当BP=BC=3时,△BCP为等腰三角形,则AP=AB-BP=2,易得t=6(s);
(3)分两种情况讨论:当P点在AC上,Q在AB上,则PC=t,BQ=2t-3,t+2t-3+3=6;当P点在AB上,Q在AC上,则AC=t-4,AQ=2t-8,t-4+2t-8=6,分别求得t的值即可.
试题解析:(1)如图1,过P作PE⊥AB,
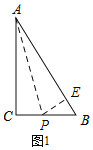
∵点P恰好在∠BAC的角平分线上,且∠C=90°,AB=5cm,BC=3cm,
∴CP=EP,
∴△ACP≌△AEP(HL),
∴AC=4cm=AE,BE=5-4=1,
设CP=x,则BP=3-x,PE=x,
∴Rt△BEP中,BE2+PE2=BP2,
即12+x2=(3-x)2
解得x=![]() ,
,
∴BP=3-![]() =
=![]() ,
,
∴CA+AB+BP=4+5+![]() =
=![]() ,
,
∴t=![]() ÷1=
÷1=![]() (s);
(s);
(2)如图2,当CP=CB时,△BCP为等腰三角形,
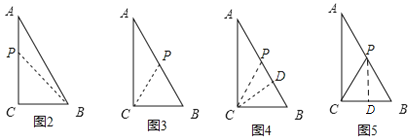
若点P在CA上,则1t=3,
解得t=3(s);
如图3,当BP=BC=3时,△BCP为等腰三角形,
∴AP=AB-BP=2,
∴t=(4+2)÷1=6(s);
如图4,若点P在AB上,CP=CB=3,作CD⊥AB于D,则根据面积法求得CD=![]() ,
,
在Rt△BCD中,由勾股定理得,BD=![]() ,
,
∴PB=2BD=![]()
∴CA+AP=4+5-![]() =5.4,
=5.4,
此时t=5.4÷1=5.4(s);
如图5,当PC=PB时,△BCP为等腰三角形,作PD⊥BC于D,则BD=CD,
∴PD为△ABC的中位线,
∴AP=BP=![]() AB=
AB=![]() ,
,
∴t=(4+![]() )÷1=
)÷1=![]() (s);
(s);
综上所述,t为3s或5.4s或6s或![]() s时,△BCP为等腰三角形;
s时,△BCP为等腰三角形;
(3)如图6,当P点在AC上,Q在AB上,则PC=t,BQ=2t-3,
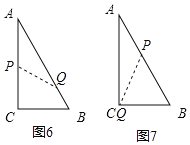
∵直线PQ把△ABC的周长分成相等的两部分,
∴t+2t-3+3=6,
∴t=2(s);
如图7,当P点在AB上,Q在AC上,则AP=t-4,AQ=2t-8,
∵直线PQ把△ABC的周长分成相等的两部分,
∴t-4+2t-8=6,
∴t=6(s);
综上所述,当t=2或6秒时,直线PQ把△ABC的周长分成相等的两部分.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
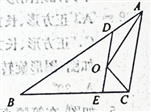
【题目】如图,在△ABC中,AB=5cm,BC=3cm,∠BAC与∠BCA的平分线相交于点O,点D在AB上,且AD=OD,DO的延长线交BC于点E.试求△BDE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC和△ADE均为等边三角形,连接BE,CD,点F,G,H分别为DE,BE,CD中点.
(1)当△ADE绕点A旋转时,如图1,则△FGH的形状为 ,说明理由;
(2)在△ADE旋转的过程中,当B,D,E三点共线时,如图2,若AB=3,AD=2,求线段FH的长;
(3)在△ADE旋转的过程中,若AB=a,AD=b(a>b>0),则△FGH的周长是否存在最大值和最小值,若存在,直接写出最大值和最小值;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好地保护美丽如画的邛海湿地,西昌市污水处理厂决定先购买A,B两种型号的污水处理设备共20台,对邛海湿地周边污水进行处理.每台A型污水处理设备12万元,每台B型污水处理设备10万元.已知1台A型污水处理设备和2台B型污水处理设备每周可以处理污水640 t,2台A型污水处理设备和3台B型污水处理设备每周可以处理污水1 080 t.
(1)求A,B两种型号的污水处理设备每周每台分别可以处理污水多少吨.
(2)经预算,市污水处理厂购买设备的资金不超过230万元,每周处理污水的量不低于4 500 t,请你列举出所有购买方案,并指出哪种方案所需资金最少,最少是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2008年5月30日,国务院关税税则委员会决定从当天起对纺织品出口关税作出进一步调整,对一些纺织品取消征收出口关税.在此背景下,某报报道了2008年1~4月份某市服装对外出口的情况,并绘制统计图如下:
请你根据统计图中提供的信息,回答下列问题:
(1)2008年1~4月份,该市服装企业出口额较多的是哪两个国家?
(2)2008年1~4月份,该市服装企业平均每月出口总额是多少万美元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线y=ax2+bx﹣2(a≠0)与x轴交于A(1,0)、B(3,0)两点,与y轴交于点C,其顶点为点D,点E的坐标为(0,﹣1),该抛物线与BE交于另一点F,连接BC.
(1)求该抛物线的解析式,并用配方法把解析式化为y=a(x﹣h)2+k的形式;
(2)若点H(1,y)在BC上,连接FH,求△FHB的面积;
(3)一动点M从点D出发,以每秒1个单位的速度平沿行与y轴方向向上运动,连接OM,BM,设运动时间为t秒(t>0),在点M的运动过程中,当t为何值时,∠OMB=90°?
(4)在x轴上方的抛物线上,是否存在点P,使得∠PBF被BA平分?若存在,请直接写出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,给出下列四个条件,AB=DE,BC=EF,∠B=∠E,∠C=∠F,从中任选三个条件能使△ABC≌△DEF的共有( )

A. 1组 B. 2组 C. 3组 D. 4组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )

A. △AFD≌△DCE B. AF=![]() AD C. AB=AF D. BE=AD﹣DF
AD C. AB=AF D. BE=AD﹣DF
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com