Question

【题目】如图，在平面直角坐标系中，已知抛物线y=ax2+bx﹣2（a≠0）与x轴交于A（1，0）、B（3，0）两点，与y轴交于点C，其顶点为点D，点E的坐标为（0，﹣1），该抛物线与BE交于另一点F，连接BC．

(1)求该抛物线的解析式，并用配方法把解析式化为y=a（x﹣h）2+k的形式；

(2)若点H（1，y）在BC上，连接FH，求△FHB的面积；

(3)一动点M从点D出发，以每秒1个单位的速度平沿行与y轴方向向上运动，连接OM，BM，设运动时间为t秒（t＞0），在点M的运动过程中，当t为何值时，∠OMB=90°？

(4)在x轴上方的抛物线上，是否存在点P，使得∠PBF被BA平分？若存在，请直接写出点P的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）y=﹣（x﹣2）2+（2） （3）t=﹣；（4）在x轴上方的抛物线上，存在点P，使得∠PBF被BA平分，P（， ）

【解析】试题分析：（1）将A、B的坐标代入y＝ax2＋bx﹣2中，得到关于a、b的二元一次方程组，求出a、b的值即可得出解析式，然后利用配方法得出顶点式即可；

（2）如图1中，先求出点F坐标，根据S△FHB＝GH×|xG－xF|＋GH×|xB－xG|计算即可；

（3）如图2中，设M（2，m），（m＞），因为OM2＝m2＋4，BM2＝m2＋1，OB2＝9，∠OMB＝90°，根据OM2＋BM2＝OB2，可得m2＋4＋m2＋1＝9，解方程即可解决问题；

（4）存在点P，使∠PBF被BA平分，在y轴上取一点N（0，1），求出直线BN的解析式为y＝x＋1，利用方程组即可求出点P坐标．

试题解析：

（1）解：∵抛物线y＝ax2＋bx﹣2（a≠0）与x轴交于A（1，0）、B（3，0）两点，

∴

∴，

∴抛物线解析式为y＝﹣x2＋x﹣2＝﹣（x﹣2）2＋ ；

（2）解：如图1，

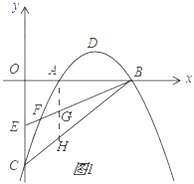
过点A作AH∥y轴交BC于H，BE于G，

由（1）有，C（0，﹣2），

∵B（0，3），

∴直线BC解析式为y＝x﹣2，

∵H（1，y）在直线BC上，

∴y＝﹣，

∴H（1，﹣ ），

∵B（3，0），E（0，﹣1），

∴直线BE解析式为y＝﹣x﹣1，

∴G（1，﹣ ），

∴GH＝，

∵直线BE：y＝﹣x﹣1与抛物线y＝﹣x2＋x﹣2相较于F，B，

∴F（，﹣），

∴S△FHB＝GH×|xG﹣xF|＋GH×|xB﹣xG|

＝GH×|xB﹣xF|

＝××（3﹣）

＝．

（3）解：如图2，

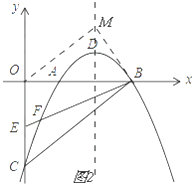
由（1）有y＝﹣x2＋x﹣2，

∵D为抛物线的顶点，

∴D（2， ），

∵一动点M从点D出发，以每秒1个单位的速度平沿行与y轴方向向上运动，

∴设M（2，m），（m＞），

∴OM2＝m2＋4，BM2＝m2＋1，AB2＝9，

∵∠OMB＝90°，

∴OM2＋BM2＝AB2 ，

∴m2＋4＋m2＋1＝9，

∴m＝或m＝﹣（舍），

∴M（0， ），

∴MD＝﹣，

∵一动点M从点D出发，以每秒1个单位的速度平沿行与y轴方向向上运动，

∴t＝﹣；

（4）解：存在点P，使∠PBF被BA平分，

如图3，

∴∠PBO＝∠EBO，

∵E（0，﹣1），

∴在y轴上取一点N（0，1），

∵B（3，0），

∴直线BN的解析式为y＝﹣x＋1①，

∵点P在抛物线y＝﹣x2＋x﹣2②上，

联立①②得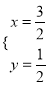， 或（舍），

∴P（， ），

即：在x轴上方的抛物线上，存在点P，使得∠PBF被BA平分，P（， ）．