
【题目】如图,在△ABC中,AB =AC,AD⊥BC于点D,AM是△ABC的外角∠CAE的平分线.
(1)求证:AM∥BC;
(2)若DN平分∠ADC交AM于点N,判断△ADN的形状并说明理由.

【答案】(1)证明见解析;(2)△ADN是等腰直角三角形,理由见解析
【解析】试题分析:(1)已知AB=AC,AD⊥BC,根据等腰三角形三线合一的性质可得∠BAD=∠CAD= ![]() ,再由AM平分∠EAC,根据角平分线的定义可得∠EAM=∠MAC=
,再由AM平分∠EAC,根据角平分线的定义可得∠EAM=∠MAC= ![]() ,根据平角的定义可得∠MAD=90°,根据同旁内角互补,两直线平行即可判定AM∥BC;(2)△ADN是等腰直角三角形,由(1)可得△ADN是直角三角形,因AM∥AD,根据平行线的性质可得∠AND=∠NDC,再由DN平分∠ADC,根据角平分线的定义和等量代换可得∠ADN=∠NDC=∠AND,根据等腰三角形的判定定理可得AD=AN,结论得证.
,根据平角的定义可得∠MAD=90°,根据同旁内角互补,两直线平行即可判定AM∥BC;(2)△ADN是等腰直角三角形,由(1)可得△ADN是直角三角形,因AM∥AD,根据平行线的性质可得∠AND=∠NDC,再由DN平分∠ADC,根据角平分线的定义和等量代换可得∠ADN=∠NDC=∠AND,根据等腰三角形的判定定理可得AD=AN,结论得证.
试题解析:
(1)∵AB=AC,AD⊥BC,
∴∠BAD=∠CAD= ![]() .
.
∵AM平分∠EAC,
∴∠EAM=∠MAC= ![]() .
.
∴∠MAD=∠MAC+∠DAC= ![]() =
=![]() .
.
∵AD⊥BC,
∴![]() ,
,
∴∠MAD+![]() ,
,
∴AM∥BC.
(2)△ADN是等腰直角三角形,
理由是:∵AM∥AD,
∴∠AND=∠NDC,
∵DN平分∠ADC,
∴∠ADN=∠NDC=∠AND.
∴AD=AN.
∴△ADN是等腰直角三角形.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线y=ax2+bx﹣2(a≠0)与x轴交于A(1,0)、B(3,0)两点,与y轴交于点C,其顶点为点D,点E的坐标为(0,﹣1),该抛物线与BE交于另一点F,连接BC.
(1)求该抛物线的解析式,并用配方法把解析式化为y=a(x﹣h)2+k的形式;
(2)若点H(1,y)在BC上,连接FH,求△FHB的面积;
(3)一动点M从点D出发,以每秒1个单位的速度平沿行与y轴方向向上运动,连接OM,BM,设运动时间为t秒(t>0),在点M的运动过程中,当t为何值时,∠OMB=90°?
(4)在x轴上方的抛物线上,是否存在点P,使得∠PBF被BA平分?若存在,请直接写出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )

A. △AFD≌△DCE B. AF=![]() AD C. AB=AF D. BE=AD﹣DF
AD C. AB=AF D. BE=AD﹣DF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是∠AOB内任意一点,且∠AOB=40°,点M和点N分别是射线OA和射线OB上的动点,当△PMN周长取最小值时,则∠MPN的度数为( )

A. 140° B. 100° C. 50° D. 40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)n边形(n>3)其中一个顶点的对角线有_____条;
(2)一个凸多边形共有14条对角线,它是几边形?
(3)是否存在有21条对角线的凸多边形?如果存在,它是几边形?如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
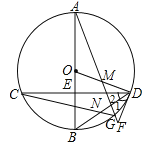
【题目】如图,在⊙O中,直径AB经过弦CD的中点E,点M在OD上,AM的延长线交⊙O于点G,交过D的直线于F,∠1=∠2,连结BD与CG交于点N.
(1)求证:DF是⊙O的切线;
(2)若点M是OD的中点,⊙O的半径为3,tan∠BOD=![]() ,求BN的长.
,求BN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在下面4×4的网格中已涂黑了三个方格,请按下面要求在网格中再涂黑一个方格.
(1)使阴影图案只是中心对称图形;
(2)使阴影图案只是轴对称图形;
(3)使阴影图案既是中心对称图形,又是轴对称图形.

查看答案和解析>>
科目:初中数学 来源: 题型:
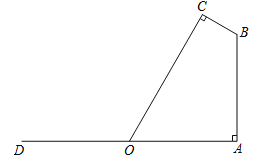
【题目】如图,若要在宽AD为20米的城南大道两边安装路灯,路灯的灯臂BC长2米,且与灯柱AB成120°角,路灯采用圆锥形灯罩,灯罩的轴线CO与灯臂BC垂直,当灯罩的轴线CO通过公路路面的中心线时照明效果最好,此时,路灯的灯柱AB高应该设计为多少米(结果保留根号)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com