练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

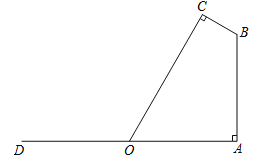
    【题目】如图，若要在宽AD为20米的城南大道两边安装路灯，路灯的灯臂BC长2米，且与灯柱AB成120°角，路灯采用圆锥形灯罩，灯罩的轴线CO与灯臂BC垂直，当灯罩的轴线CO通过公路路面的中心线时照明效果最好，此时，路灯的灯柱AB高应该设计为多少米（结果保留根号）？

    【答案】．

    【解析】试题分析：延长OC，AB交于点P，△PCB∽△PAO，根据相似三角形对应边比例相等的性质即可解题．

    试题解析：解：如图，延长OC，AB交于点P．

    ∵∠ABC=120°，∴∠PBC=60°，∵∠OCB=∠A=90°，∴∠P=30°，∵AD=20米，∴OA=AD=10米，∵BC=2米，∴在Rt△CPB中，PC=BCtan60°=米，PB=2BC=4米，∵∠P=∠P，∠PCB=∠A=90°，∴△PCB∽△PAO，∴，∴PA===米，∴AB=PA﹣PB=（）米．

    答：路灯的灯柱AB高应该设计为（）米．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB ＝AC，AD⊥BC于点D，AM是△ABC的外角∠CAE的平分线．

    (1)求证：AM∥BC；

    (2)若DN平分∠ADC交AM于点N，判断△ADN的形状并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知, 是直线上的点， ，过点作,并截取 ,连接 ，判断△的形状并证明.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某学校初一年级参加社会实践课，报名第一门课的有x人，第二门课的人数比第一门课的少10人，现在需要从报名第二门课的人中调出10人学习第一门课，那么：

    （1）报两门课的共有多少人？

    （2）调动后，报名第一门课的人数为　 　人，第二门课人数为　 　人．

    （3）调动后，报名第一门课比报名第二门课多多少人？计算出代数式后，请选择一个你觉得合适的x的值代入，并求出具体的人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】你能求（x﹣1）（x99+x98+x97+…+x+1）的值吗？遇到这样的问题，我们可以先思考一下，从简单的情形入手．先分别计算下列各式的值：

    ①（x﹣1）（x+1）=x2﹣1；

    ②（x﹣1）（x2+x+1）=x3﹣1；

    ③（x﹣1）（x3+x2+x+1）=x4﹣1；

    …

    由此我们可以得到：（x﹣1）（x99+x98+x97+…+x+1）= ．

    请你利用上面的结论，再完成下面两题的计算：

    （1）（﹣2）50+（﹣2）49+（﹣2）48+…+（﹣2）+1．

    （2）若x3+x2+x+1=0，求x2016的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，抛物线（a≠0）与x轴交于A、B两点，与y轴交于点C，且OA=2，OB=8，OC=6．

    （1）求抛物线的解析式；

    （2）点M从A点出发，在线段AB上以每秒3个单位长度的速度向B点运动，同时，点N从B出发，在线段BC上以每秒1个单位长度的速度向C点运动，当其中一个点到达终点时，另一个点也停止运动，当△MBN存在时，求运动多少秒使△MBN的面积最大，最大面积是多少？

    （3）在（2）的条件下，△MBN面积最大时，在BC上方的抛物线上是否存在点P，使△BPC的面积是△MBN面积的9倍？若存在，求点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】求下列各式中的值：

    （1） ；（2）.

    【答案】（1）2 ；（2）3.

    【解析】试题分析：（1）、（2）都是把方程两边的底数变为相同的，根据指数相等得到有关n的方程，然后解方程即可得.

    试题解析：（1）27n=3n+4，

    （33）n=3n+4，

    33n=3n+4，

    所以，3n=n+4，

    n=2；

    （2），

    2×（23）n×(24)n=222，

    2×23n×24n=222，

    21+3n+4n=222，

    所以，1+3n+4n=22，

    n=3.

    【题型】解答题
    【结束】
    21

    【题目】一个多边形的所有内角与它的一个外角之和是2018°，求这个外角的度数和它的边数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，每个小正方形边长为1，点A的坐标为(－2，3)、点B的坐标为(－3，1)、点C的坐标为(1，-2)

    (1)作出△ABC关于y轴对称的△A′B′C′（其中A′、B′、C′分别是A、B、C的对应点，不写画法）.

    (2) 直接写出A′、B′、C三点的坐标.

    (3)在x轴上求作一点P，使PA+PB的值最小.（简要写出作图步骤）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某中学七（2）班学生去劳动实践基地开展实践劳动，在劳动前需要分成x组，若每组11人，则余下一人，若每组12人，则有一组少4人，若每组分配7人，则该班可分成_____组．

    查看答案和解析>>

    同步练习册答案