
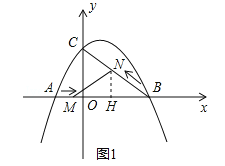
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������![]() ��a��0����x�ύ��A��B���㣬��y�ύ�ڵ�C����OA=2��OB=8��OC=6��
��a��0����x�ύ��A��B���㣬��y�ύ�ڵ�C����OA=2��OB=8��OC=6��
��1���������ߵĽ���ʽ��
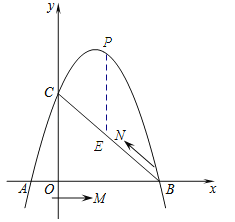
��2����M��A����������߶�AB����ÿ��3����λ���ȵ��ٶ���B���˶���ͬʱ����N��B���������߶�BC����ÿ��1����λ���ȵ��ٶ���C���˶���������һ���㵽���յ�ʱ����һ����Ҳֹͣ�˶�������MBN����ʱ�����˶�������ʹ��MBN���������������Ƕ��٣�
��3���ڣ�2���������£���MBN������ʱ����BC�Ϸ������������Ƿ���ڵ�P��ʹ��BPC���������MBN�����9���������ڣ����P�����ꣻ�������ڣ���˵�����ɣ�

���𰸡���1��![]() ����2���˶�
����2���˶�![]() ��ʹ��MBN����������������
��ʹ��MBN����������������![]() ����3��P��3��
����3��P��3�� ![]() ����5��
����5�� ![]() ����
����
�������������������1�����߶εij��ȵó���A��B��C�����꣬Ȼ���A��B��C���������ֱ����![]() ���ⷽ���飬���ɵ������ߵĽ���ʽ��
���ⷽ���飬���ɵ������ߵĽ���ʽ��
��2�����˶�ʱ��Ϊt�룬��MB=6��3t��Ȼ�������BHN�ס�BOC�����NH=![]() t�������������ε������ʽ�г�S��MBN��t�ĺ�����ϵʽS��MBN=��
t�������������ε������ʽ�г�S��MBN��t�ĺ�����ϵʽS��MBN=��![]() ��t��
��t��![]() ��2+
��2+![]() �����ö��κ�����ͼ�����ʽ��н��
�����ö��κ�����ͼ�����ʽ��н��
��3�����ô���ϵ�������ֱ��BC�Ľ���ʽΪ![]() ���ɶ��κ���ͼ���ϵ���������������P������Ϊ��m��
���ɶ��κ���ͼ���ϵ���������������P������Ϊ��m�� ![]() ��������P��PE��y�ᣬ��BC�ڵ�E�������֪�����ͣ�2���еĽ�����S��PBC=
��������P��PE��y�ᣬ��BC�ڵ�E�������֪�����ͣ�2���еĽ�����S��PBC=![]() �������ͼ�εõ�S��PBC=S��CEP+S��BEP=
�������ͼ�εõ�S��PBC=S��CEP+S��BEP=![]() EPm+
EPm+![]() EP��8��m����������߶εij��ȴ�����֪��
EP��8��m����������߶εij��ȴ�����֪�� ![]() =
=![]() ��
��
����������⣺��1����OA=2��OB=8��OC=6�������ݺ���ͼ���A����2��0����B��8��0����C��0��6��������������� 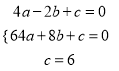 �������
������� 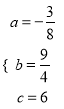 ���������ߵĽ���ʽΪ
���������ߵĽ���ʽΪ
��2�����˶�ʱ��Ϊt�룬��AM=3t��BN=t����MB=10��3t��������ã���C������Ϊ��0��6������Rt��BOC�У�BC=![]() =10����ͼ������N��NH��AB�ڵ�H����NH��CO�����BHN�ס�BOC����
=10����ͼ������N��NH��AB�ڵ�H����NH��CO�����BHN�ס�BOC����![]() ����
����![]() ����HN=
����HN=![]() t����S��MBN=
t����S��MBN=![]() MBHN=
MBHN=![]() ��10��3t��
��10��3t��![]() t=
t=![]() =��
=��![]() ��t��
��t��![]() ��2+
��2+![]() ������MBN����ʱ��0��t��2������t=
������MBN����ʱ��0��t��2������t=![]() ʱ��S��MBN���=
ʱ��S��MBN���=![]() ��
��
���˶�![]() ��ʹ��MBN����������������
��ʹ��MBN����������������![]() ��
��
��3����ֱ��BC�Ľ���ʽΪy=kx+c��k��0����
��B��8��0����C��0��6�����룬���� ![]() �������
������� 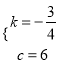 ����ֱ��BC�Ľ���ʽΪ
����ֱ��BC�Ľ���ʽΪ![]() ��
��
����P���������ϣ������P������Ϊ��m�� ![]() ������ͼ������P��PE��y�ᣬ��BC�ڵ�E����E�������Ϊ��m��
������ͼ������P��PE��y�ᣬ��BC�ڵ�E����E�������Ϊ��m�� ![]() ����
����
��EP=![]() ����
����![]() ��=
��=![]() ������MBN��������ʱ��S��PBC=9 S��MBN=
������MBN��������ʱ��S��PBC=9 S��MBN=![]() ����S��PBC=S��CEP+S��BEP=
����S��PBC=S��CEP+S��BEP=![]() EPm+
EPm+![]() EP��8��m��=
EP��8��m��=![]() ��8EP=4����
��8EP=4����![]() ��=
��=![]() ����
����![]() =
=![]() �����m1=3��m2=5����P��3��
�����m1=3��m2=5����P��3�� ![]() ����5��
����5�� ![]() ����
����


 ǧ�������������ĩ�����Ծ�����ϵ�д�
ǧ�������������ĩ�����Ծ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1)n����(n��3)����һ������ĶԽ�����_____����
(2)һ������ι���14���Խ���,���Ǽ�������
(3)�Ƿ������21���Խ��ߵ�����Σ��������,���Ǽ����Σ����������,˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪ABΪ��O��ֱ����AD��BD����O���ң�BC����O�����ߣ��е�ΪB��OC��AD��BA��CD���ӳ����ཻ�ڵ�E��
��1����֤��DC����O�����ߣ�
��2����AE=1��ED=3������O�İ뾶��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����գ���ͼ������ֽ��ÿ��С�����εı߳���Ϊ1���ڷ���ֽ�ڽ���ABC����һ��ƽ�ƺ�õ���A��B��C�䣬ͼ�б���˵�B�Ķ�Ӧ��B�䣮

��1���ڸ�������ֽ�л���ƽ�ƺ����A��B��C�䣻
��2������AB���ϵ�����CD��BC���ϵĸ���AE��
��3���߶�AA�����߶�BB��Ĺ�ϵ�ǣ� ��
��4�����ı���ACBB��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
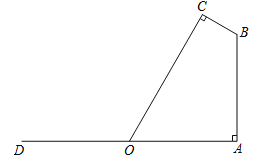
����Ŀ����ͼ����Ҫ�ڿ�ADΪ20�ij��ϴ�����߰�װ·�ƣ�·�ƵĵƱ�BC��2�ף��������AB��120���ǣ�·�Ʋ���Բ�ε��֣����ֵ�����CO��Ʊ�BC��ֱ�������ֵ�����COͨ����··���������ʱ����Ч����ã���ʱ��·�Ƶĵ���AB��Ӧ�����Ϊ�����ף�����������ţ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����ABC�͡�ACB��ƽ���߽��ڵ�O��EF������O��ƽ����BC���ֱ���AB��AC���ڵ�E��F��
(1)����ABC��50������ACB��60�������BOC�Ķ�����
(2)����ABC������ACB���������Ĵ���ʽ��ʾ��BOC�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��ƽ��ȥ�آ�Բ����Բ�����������������ܵõ��Ľ�����Բ��ͼ���ǣ� ��
A.�ڢ�B.�٢ڢ�C.�ڢۢ�D.�٢ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����A�ǰ�Բ�ϵ�һ�����ȷֵ㣬B���ӻ�![]() ���е㣬��P��ֱ��MN�ϵ�һ�����㣬��O�İ뾶Ϊ1����AP+PB����Сֵ_______��
���е㣬��P��ֱ��MN�ϵ�һ�����㣬��O�İ뾶Ϊ1����AP+PB����Сֵ_______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪DC��FP����1����2����FED��28����AGF��80��FHƽ�֡�EFG��
(1)˵����DC��AB��
(2)���PFH�Ķ�����

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com