练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】用一个平面去截①圆锥、②圆柱、③球、④五棱柱，能得到的截面是圆的图形是（ ）

    A.②④B.①②③C.②③④D.①③④

    【答案】B

    【解析】

    根据圆锥、圆柱、球、五棱柱的形状特点逐一判断即可．

    如果截面与圆锥底面平行，那么截面是圆，故①符合题意，

    如果截面与圆柱的上下面平行，那么截面是圆，故②符合题意，

    用一个平面去截球，截面一定是圆，故③符合题意，

    用一个平面去截五棱柱，无论怎么去截，截面都不可能有弧度，故④不符合题意，

    综上所述：能得到的截面是圆的图形是①②③，

    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，已知抛物线过点A（﹣3，0），B（﹣2，3），C（0，3），其顶点为D．

    （1）求抛物线的解析式；

    （2）设点M（1，m），当MB+MD的值最小时，求m的值；

    （3）若P是抛物线上位于直线AC上方的一个动点，求△APC的面积的最大值；

    （4）若抛物线的对称轴与直线AC相交于点N，E为直线AC上任意一点，过点E作EF∥ND交抛物线于点F，以N，D，E，F为顶点的四边形能否为平行四边形？若能，求点E的坐标；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某学校初一年级参加社会实践课，报名第一门课的有x人，第二门课的人数比第一门课的少10人，现在需要从报名第二门课的人中调出10人学习第一门课，那么：

    （1）报两门课的共有多少人？

    （2）调动后，报名第一门课的人数为　 　人，第二门课人数为　 　人．

    （3）调动后，报名第一门课比报名第二门课多多少人？计算出代数式后，请选择一个你觉得合适的x的值代入，并求出具体的人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，抛物线（a≠0）与x轴交于A、B两点，与y轴交于点C，且OA=2，OB=8，OC=6．

    （1）求抛物线的解析式；

    （2）点M从A点出发，在线段AB上以每秒3个单位长度的速度向B点运动，同时，点N从B出发，在线段BC上以每秒1个单位长度的速度向C点运动，当其中一个点到达终点时，另一个点也停止运动，当△MBN存在时，求运动多少秒使△MBN的面积最大，最大面积是多少？

    （3）在（2）的条件下，△MBN面积最大时，在BC上方的抛物线上是否存在点P，使△BPC的面积是△MBN面积的9倍？若存在，求点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】求下列各式中的值：

    （1） ；（2）.

    【答案】（1）2 ；（2）3.

    【解析】试题分析：（1）、（2）都是把方程两边的底数变为相同的，根据指数相等得到有关n的方程，然后解方程即可得.

    试题解析：（1）27n=3n+4，

    （33）n=3n+4，

    33n=3n+4，

    所以，3n=n+4，

    n=2；

    （2），

    2×（23）n×(24)n=222，

    2×23n×24n=222，

    21+3n+4n=222，

    所以，1+3n+4n=22，

    n=3.

    【题型】解答题
    【结束】
    21

    【题目】一个多边形的所有内角与它的一个外角之和是2018°，求这个外角的度数和它的边数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列正确说法的是____

    ①同位角相等； ②等角的补角相等； ③两直线平行，同旁内角相等；④在同一平面内，过一点有且只有一条直线与已知直线垂直．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，每个小正方形边长为1，点A的坐标为(－2，3)、点B的坐标为(－3，1)、点C的坐标为(1，-2)

    (1)作出△ABC关于y轴对称的△A′B′C′（其中A′、B′、C′分别是A、B、C的对应点，不写画法）.

    (2) 直接写出A′、B′、C三点的坐标.

    (3)在x轴上求作一点P，使PA+PB的值最小.（简要写出作图步骤）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知,如图, AB∥CD，∠1=∠2，那么∠E和∠F相等吗? 为什么?

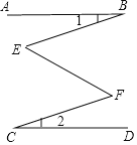
    【答案】相等，理由见解析.

    【解析】试题分析：分别过E、F 点作CD的平行线EM、FN，根据平行线的性质得CD∥FN∥EM∥AB，则∠3=∠1，∠4=∠5，∠1=∠6，而∠1=∠2，于是3+∠4=∠5+∠6．

    试题解析：分别过E、F 点作CD的平行线EM、FN，如图

    ∵AB∥CD，

    ∴CD∥FN∥EM∥AB，

    ∴∠3=∠2，∠4=∠5，∠1=∠6，

    而∠1=∠2，

    ∴∠3+∠4=∠5+∠6，

    即∠BEF=∠EFC．

    【题型】解答题
    【结束】
    26

    【题目】(1)填空21－20＝2( )； 22－21＝2( ) ；23 －22＝2( )

    (2)请用字母表示第n个等式，并验证你的发现．

    (3)利用(2)中你的发现，求20＋21＋22＋23＋…＋22016＋22017的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB∥CD，OE平分∠BOC，OF⊥OE，OP⊥CD，∠ABO=40°，则下列结论：

    ①∠BOE=70°; ②OF平分∠BOD;③∠POE=∠BOF; ④∠POB=2∠DOF.

    其中正确的结论有_______________（填结论前面的序号）

    查看答案和解析>>

    同步练习册答案