
【题目】如图,已知AB为⊙O的直径,AD、BD是⊙O的弦,BC是⊙O的切线,切点为B,OC∥AD,BA、CD的延长线相交于点E.
(1)求证:DC是⊙O的切线;
(2)若AE=1,ED=3,求⊙O的半径.

【答案】(1)证明见解析;(2)4.
【解析】试题分析:(1)、连接DO,根据平行线的性质得出∠DAO=∠COB,∠ADO=∠COD,结合OA=OD得出∠COD=∠COB,从而得出△COD和△COB全等,从而得出切线;(2)、设⊙O的半径为R,则OD=R,OE=R+1,根据Rt△ODE的勾股定理求出R的值得出答案.
试题解析:(1)证明:连结DO. ∵AD∥OC, ∴∠DAO=∠COB,∠ADO=∠COD.
又∵OA=OD, ∴∠DAO=∠ADO, ∴∠COD=∠COB.
在△COD和△COB中 ∵OD=OB,OC=OC, ∴△COD≌△COB(SAS),
∴∠CDO=∠CBO. ∵BC是⊙O的切线, ∴∠CBO=90°, ∴∠CDO=90°,
又∵点D在⊙O上, ∴CD是⊙O的切线;
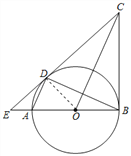
(2)设⊙O的半径为R,则OD=R,OE=R+1, ∵CD是⊙O的切线, ∴∠EDO=90°,
∴ED2+OD2=OE2, ∴32+R2=(R+1)2, 解得R=4, ∴⊙O的半径为4.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】甲组的4名工人3月份完成的总工作量比此月人均定额的4倍多20件,乙组的5名工人3月份完成的总工作量比此月人均定额的6倍少20件.
(1)如果两组工人实际完成的此月人均工作量相等,那么此月人均定额是多少件?
(2)如果甲组工人实际完成的此月人均工作量比乙组的多2件,则此月人均定额是多少件?
(3)如果甲组工人实际完成的此月人均工作量比乙组的少2件,则此月人均定额是多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 过点A(﹣3,0),B(﹣2,3),C(0,3),其顶点为D.
过点A(﹣3,0),B(﹣2,3),C(0,3),其顶点为D.
(1)求抛物线的解析式;
(2)设点M(1,m),当MB+MD的值最小时,求m的值;
(3)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值;
(4)若抛物线的对称轴与直线AC相交于点N,E为直线AC上任意一点,过点E作EF∥ND交抛物线于点F,以N,D,E,F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列材料:
我们已经学过将一个多项式分解因式的方泫有提公因式法和运用公式法,其实分解因式的方法还有分组分解法、拆项法、十字相乘法等等.
(1)分组分解法:将一个多项式适当分组后,可提公因式或运用公式继续分解的方法.
如: ![]() ,
, ![]()
分组分解法:
解:原式![]() 解:原式
解:原式![]()
![]()
![]()
![]()
(2)拆项法:将一个多项式的某一项拆成两项后,可提公因式或运用公式继续分解的方法.
如: ![]()
解:原式![]()
![]()
![]()
![]()
请你仿照以上方法,探索并解决下列问题:
(l)分解因式: ![]() ;
;
(2)分解因式: ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校初一年级参加社会实践课,报名第一门课的有x人,第二门课的人数比第一门课的![]() 少10人,现在需要从报名第二门课的人中调出10人学习第一门课,那么:
少10人,现在需要从报名第二门课的人中调出10人学习第一门课,那么:
(1)报两门课的共有多少人?
(2)调动后,报名第一门课的人数为 人,第二门课人数为 人.
(3)调动后,报名第一门课比报名第二门课多多少人?计算出代数式后,请选择一个你觉得合适的x的值代入,并求出具体的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() (a≠0)与x轴交于A、B两点,与y轴交于点C,且OA=2,OB=8,OC=6.
(a≠0)与x轴交于A、B两点,与y轴交于点C,且OA=2,OB=8,OC=6.
(1)求抛物线的解析式;
(2)点M从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时,点N从B出发,在线段BC上以每秒1个单位长度的速度向C点运动,当其中一个点到达终点时,另一个点也停止运动,当△MBN存在时,求运动多少秒使△MBN的面积最大,最大面积是多少?
(3)在(2)的条件下,△MBN面积最大时,在BC上方的抛物线上是否存在点P,使△BPC的面积是△MBN面积的9倍?若存在,求点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图, AB∥CD,∠1=∠2,那么∠E和∠F相等吗? 为什么?
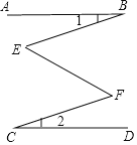
【答案】相等,理由见解析.
【解析】试题分析:分别过E、F 点作CD的平行线EM、FN,根据平行线的性质得CD∥FN∥EM∥AB,则∠3=∠1,∠4=∠5,∠1=∠6,而∠1=∠2,于是3+∠4=∠5+∠6.
试题解析:分别过E、F 点作CD的平行线EM、FN,如图
∵AB∥CD,
∴CD∥FN∥EM∥AB,
∴∠3=∠2,∠4=∠5,∠1=∠6,
而∠1=∠2,
∴∠3+∠4=∠5+∠6,
即∠BEF=∠EFC.

【题型】解答题
【结束】
26
【题目】(1)填空21-20=2( ); 22-21=2( ) ;23 -22=2( )
(2)请用字母表示第n个等式,并验证你的发现.
(3)利用(2)中你的发现,求20+21+22+23+…+22016+22017的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com