
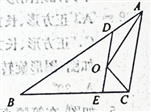
【题目】如图,在△ABC中,AB=5cm,BC=3cm,∠BAC与∠BCA的平分线相交于点O,点D在AB上,且AD=OD,DO的延长线交BC于点E.试求△BDE的周长.
【答案】8cm
【解析】试题分析:根据等腰三角形的性质和角平分线的定义易证∠DOA=∠OAC,即可得DE∥AC,再由角平分线的定义和平行线的性质证得∠EOC=∠ECO,根据等腰三角形的性质可得OE=CE,再由BE+DE+BD=BE+OE+OD+BD=BE+EC+BD+DA=AB+BC即可得△BDE的周长.
试题解析:
∵AD=OD,
∴∠DAO=∠DOA,
∵∠DAO=∠OAC,
∴∠DOA=∠OAC,
∴DE∥AC,
∴∠EOC=∠OCA,
∵∠OCA=∠OCE,
∴∠EOC=∠ECO,
∴OE=CE,
∴BE+DE+BD=BE+OE+OD+BD=BE+EC+BD+DA=AB+BC=5+3=8(cm),
∴△BDE的周长=8cm.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】直线AB、CD相交于点O,OE平分∠BOD,OF⊥CD,垂足为O.
(1)若∠EOF=54°,求∠AOC的度数;
(2)①在∠AOD的内部作射线OG⊥OE;
②试探索∠AOG与∠EOF之间有怎样的关系?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=∠ACB=72°,CD平分∠ACB,则∠ADC=______.图中有______个等腰三角形,它们是:_________________________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知A(1,-5),B(4,2),C(-1,0)三点.
(1)点B关于x轴对称点B′的坐标为 ,点C关于y轴对称点C′的坐标为 ;
(2)求(1)中的△AB′C′的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB与x轴,y轴交于点A(10,0),B(0,-10),直线MT垂直于直线AB,垂足为M,与y轴交于点T(0,-2) .
(1)求点M的坐标;
(2)在线段MT的延长线上找一点N,使MT=TN,求点N的坐标;
(3)若点D在x轴上,∠ABD=60°,E点在线段BD上运动,∠AEB的平分线交AB于点P,∠EAB的平分线交线段BD于点Q,AQ与EP交于点R. ![]() 的值是多少?
的值是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( )
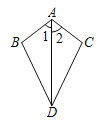
A. AB=AC B. BD=CD C. ∠B=∠C D. ∠BDA=∠CDA
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于有理数x,y定义新运算:x*y=ax+by -5,其中a,b为常数.已知1*2=9,(-3)*3=-2,则a-b=
A.-1B.1C.-2D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
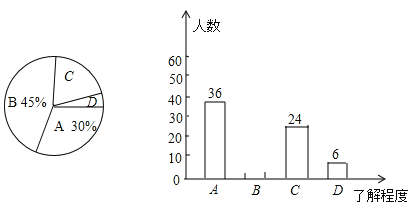
【题目】今年市委市政府积极推进创建“全国文明城市”工作,市创城办公室为了调查初中学生对“社会主义核心价值观”内容的了解程度(程度分为:“A﹣十分熟悉”,“B﹣了解较多”,“C﹣了解较少”,“D﹣不知道”),对我市一所中学的学生进行了随机抽样调查,根据调查结果绘制了两幅不完整的统计图如图,根据信息解答下列问题:
(1)本次抽样调查了多少名学生;
(2)补全条形统计图和扇形统计图;
(3)求扇形统计图中“D﹣不知道”所在的扇形圆心角的度数;
(4)若该中学共有2400名学生,请你估计这所中学的所有学生中,对“社会主义核心价值观”内容的了解程度为“十分熟悉”和“了解较多”的学生共有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=Rt∠,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.

(1)出发2秒后,求△ABP的周长.
(2)问t满足什么条件时,△BCP为直角三角形?
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com