
【题目】如图,在平面直角坐标系中,直线AB与x轴,y轴交于点A(10,0),B(0,-10),直线MT垂直于直线AB,垂足为M,与y轴交于点T(0,-2) .
(1)求点M的坐标;
(2)在线段MT的延长线上找一点N,使MT=TN,求点N的坐标;
(3)若点D在x轴上,∠ABD=60°,E点在线段BD上运动,∠AEB的平分线交AB于点P,∠EAB的平分线交线段BD于点Q,AQ与EP交于点R. ![]() 的值是多少?
的值是多少?

【答案】(1)M(4,-6)(2)N(-4,2)(3)1
【解析】试题分析:(1)M点可以看作是直线AB与直线MN的交点,要求交点坐标即要求出这两条直线的解析式,已知A、B的坐标可以求出直线AB的解析式,结合特殊角可以求出OC的长度,从而求出C的坐标,根据C、T的坐标可以求出直线MN的解析式;(2)作MG⊥y轴于点G,NH⊥y轴于点H,结合已知条件不难证明△NHT≌△MGT,进而求出NH、HO的长度,表示出N的坐标即可;(3)在AE上取一点G,使EQ=EG ,不难证明△ERG≌△ERQ,由此可得∠EGR=∠ERQ,再由∠AEB的平分线交AB于点P,∠EAB的平分线交线段BD于点Q,∠ABD=60°可以计算得出∠ERA=120°,进而可以得出∠ERQ=60°,所以∠GRA=∠PRA=60°,接下去不难证明△ARG≌△ARP,可以得出AP=AG,所以![]() =
=![]() =1.
=1.
试题解析:
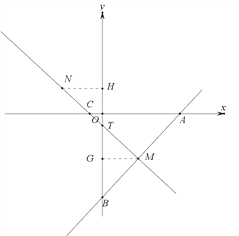
(1)∵A(10,0),B(0,-10),
∴AO=BO=10,
∴∠OBA=45°,
∵MN⊥AB,
∴∠TMB=90°,
∴∠BTM=∠CTO=45°,
∴CO=TO,
∵T(0,-2),
∴CO=TO=2,
∴C(-2,0),
设y=k1x+b1,
![]() ,
,
∴![]() ,
,
∴y=-x-2,
设直线AB解析式为y2=k2x+b2,
![]() ,
,
∴![]() ,
,
∴y=x-10,
![]() ,
,
解得![]() ,
,
∴M(4,-6);
(2)作MG⊥y轴于点G,NH⊥y轴于点H,
∴∠NHT=∠MGT=90°,
∵在△NHT和△MGT中,
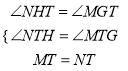 ,
,
∴△NHT≌△MGT,
∴NH=MG=4,HT=GT=4,
∴HO=2,
∴N(-4,2);
(3)
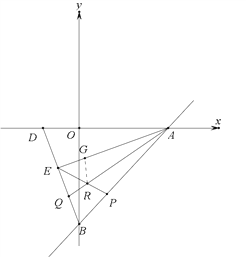
在AE上取一点G,使EQ=EG ,
∵PE平分∠AEB,QA平分∠EAB,
∴∠AER=![]() ∠AEB,∠EAR=
∠AEB,∠EAR=![]() ∠EAB,
∠EAB,
∴∠AER+∠EAR =![]() (∠AEB+∠EAB),
(∠AEB+∠EAB),
∵∠ABD=60°,
∴∠AEB+∠EAB=120°,
∴∠AER+∠EAR=60°,
∴∠ERA=120°,
∴∠ERQ=60°,
∵PE平分∠AEB,
∴∠GER=∠QER,
∵在△GER和△QER中,
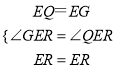 ,
,
∴△GER≌△QER,
∴∠ERG=∠ERQ=60°,
∴∠ARG=60°,∠ARP=60°,
∵在△ARG和△ARP中,
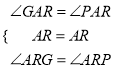 ,
,
∴△ARG≌△ARP,
∴AP=AG,
∴![]() =
=![]() =1.
=1.


科目:初中数学 来源: 题型:
【题目】一艘货轮往返于上下游两个码头之间,逆流而上需要6小时,顺流而下需要4小时,若船在静水中的速度为20千米/时,则水流的速度是_____千米/时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D是BC的中点,点E在AD上,BE的延长线交AC于点F,且BF⊥AC,垂足为F,∠BAC=45°
求证:△AEF≌△BCF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=5cm,BC=3cm,∠BAC与∠BCA的平分线相交于点O,点D在AB上,且AD=OD,DO的延长线交BC于点E.试求△BDE的周长.
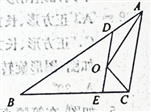
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下面推理过程补充完整,在括号内注明理由:
已知:如图,BC//EF,AB=DE,BC=EF,试说明∠C=∠F;
解:∵BC//EF(已知)
∴∠ABC=∠__________ _________________________
在△ABC与△DEF中,
∵
∴△ABC≌△DEF _______
∴∠C=∠F ____________________________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2008年5月30日,国务院关税税则委员会决定从当天起对纺织品出口关税作出进一步调整,对一些纺织品取消征收出口关税.在此背景下,某报报道了2008年1~4月份某市服装对外出口的情况,并绘制统计图如下:
请你根据统计图中提供的信息,回答下列问题:
(1)2008年1~4月份,该市服装企业出口额较多的是哪两个国家?
(2)2008年1~4月份,该市服装企业平均每月出口总额是多少万美元?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com