
【题目】如图,![]() 中,
中, ![]() ,
,![]() ,将
,将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在直角边
落在直角边![]() 上的
上的![]() 点处,设
点处,设![]() 与
与![]() 边分别交于点
边分别交于点![]() ,如果折叠后
,如果折叠后![]() 与
与![]() 均为等腰三角形,那么
均为等腰三角形,那么![]() __________.
__________.

【答案】![]() 或
或![]()
【解析】
先确定△CDF是等腰三角形,得出∠CFD=∠CDF=45°,因为不确定△BDE是以那两条边为腰的等腰三角形,故需讨论,①DE=DB,②BD=BE,③DE=BE,然后分别利用角的关系得出答案即可.
∵△CDF中,∠C=90°,且△CDF是等腰三角形,
∴CF=CD,
∴∠CFD=∠CDF=45°,
设∠DAE=x°,由对称性可知,AF=FD,AE=DE,
∴∠FDA=![]() ∠CFD=22.5°,∠DEB=2x°,
∠CFD=22.5°,∠DEB=2x°,
分类如下:
①如图1,
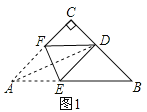
当DE=DB时,∠B=∠DEB=2x°,
由∠CDE=∠DEB+∠B,得45°+22.5°+x=4x,
解得:x=22.5°.此时∠B=2x=45°;
②,如图2,
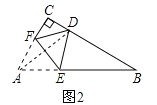
当BD=BE时,则∠B=(180°-4x)°,
由∠CDE=∠DEB+∠B得:45°+22.5°+x=2x+180°-4x,
解得x=37.5°,此时∠B=(180-4x)°=30°.
综上所述∠B=45°或30°.
故答案为:45°或30°


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:
【题目】先阅读下面例题的解法,然后解答问题:
例:若多项式2x3-x2+m分解因式的结果中有因式2x+1,求实数m的值.
解:设2x3-x2+m=(2x+1)·A(A为整式).
若2x3-x2+m=(2x+1)·A=0,则2x+1=0或A=0.
由2x+1=0,解得x=-![]() .
.
∴x=-![]() 是方程2x3-x2+m=0的解.
是方程2x3-x2+m=0的解.
∴2×(-![]() )3-(-
)3-(-![]() )2+m=0,即-
)2+m=0,即-![]() -
-![]() +m=0.
+m=0.
∴m=![]() .
.
请你模仿上面的方法尝试解决下面的问题:
若多项式x4+mx3+nx-16分解因式的结果中有因式(x-1)和(x-2),求实数m,n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形,∠BAD的角平分线AF交CD于点E,交BC的延长线于点F. 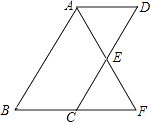
(1)求证:BF=CD;
(2)连接BE,若BE⊥AF,∠BFA=60°,BE=2 ![]() ,求平行四边形ABCD的周长.
,求平行四边形ABCD的周长. 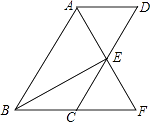
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,OP是∠MON的平分线,请你利用该图形画一对以OP所在直线为对称轴的全等三角形,并将添加的全等条件标注在图上.
请你参考这个作全等三角形的方法,解答下列问题:
(1)如图2,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC和∠BCA的平分线,AD、CE相交于点F,求∠EFA的度数;
(2)在(1)的条件下,请判断FE与FD之间的数量关系,并说明理由;
(3)如图3,在△ABC中,如果∠ACB不是直角,而( 1 )中的其他条件不变,试问在(2)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰△ABC中,
(1)如图1,若△ABC为等边三角形,D为线段BC中点,线段AD关于直线AB的对称线段为线段AE,连接DE,则∠BDE的度数为;
(2)若△ABC为等边三角形,点D为线段BC上一动点(不与B,C重合),连接AD并将 线段AD绕点D逆时针旋转60°得到线段DE,连接BE.
①根据题意在图2中补全图形;
②小玉通过观察、验证,提出猜测:在点D运动的过程中,恒有CD=BE.经过与同学们的充分讨论,形成了几种证明的思路:
思路1:要证明CD=BE,只需要连接AE,并证明△ADC≌△AEB;
思路2:要证明CD=BE,只需要过点D作DF∥AB,交AC于F,证明△ADF≌△DEB;
思路3:要证明CD=BE,只需要延长CB至点G,使得BG=CD,证明△ADC≌△DEG;
…
请参考以上思路,帮助小玉证明CD=BE.(只需要用一种方法证明即可)
(3)小玉的发现启发了小明:如图3,若AB=AC=kBC,AD=kDE,且∠ADE=∠C,此时小明发现BE,BD,AC三者之间满足一定的数量关系,这个数量关系是 . (直接给出结论无须证明)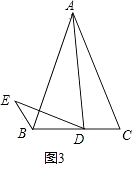
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在平面直角坐标系中,![]() 的顶点
的顶点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() 的坐标为
的坐标为![]() .
.
(1)请你在所给的平面直角坐标系中,画出![]() 关于
关于![]() 轴对称的
轴对称的![]() ;
;
(2)将(1)中得到的![]() 向下移动4个单位得到
向下移动4个单位得到![]() ,画出
,画出![]() ;
;
(3)在![]() 中有一点
中有一点![]() ,直接写出经过以上两次图形变换后
,直接写出经过以上两次图形变换后![]() 中对应点
中对应点![]() 的坐标.
的坐标.
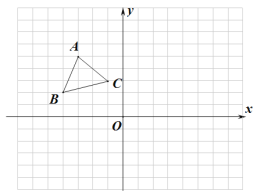
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C、D两点将线段AB分为三部分,AC:CD:DB=2:3:4,且AC=4.M是线段AB的中点,N是线段DB的中点.
(1)求线段DB、AB的长.
(2)求线段MN的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
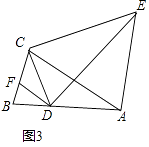
【题目】已知△ABC中,D为AB边上任意一点,DF∥AC交BC于F,AE∥BC,∠CDE=∠ABC=∠ACB=α.
(1)如图1,当α=60°时,求证:△DCE是等边三角形;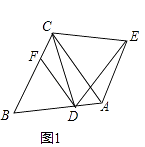
(2)如图2,当α=45°时,求证:① ![]() =
= ![]() ;②CE⊥DE.
;②CE⊥DE.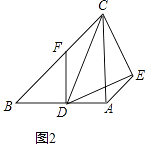
(3)如图3,当α为任意锐角时,请直接写出线段CE与DE的数量关系是: ![]() = .
= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆某中学组织七、八、九年级学生参加“直辖20年,点赞新重庆”作文比赛,该校将收到的参赛作文进行分年级统计,绘制了如图1和如图2两幅不完整的统计图,根据图中提供的信息完成以下问题. 
(1)扇形统计图中九年级参赛作文篇数对应的圆心角是度,并补全条形统计图;
(2)经过评审,全校有4篇作文荣获特等奖,其中有一篇来自七年级,学校准备从特等奖作文中任选两篇刊登在校刊上,请利用画树状图或列表的方法求出七年级特等奖作文被选登在校刊上的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com