
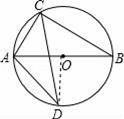
如图,⊙O的直径为8cm,∠B=30°,∠ACB的平分线交⊙O于D,连接AD.
(1)求BC的长;
(2)求∠CAD的度数.
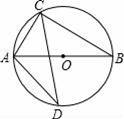

【考点】圆周角定理.
【分析】(1)由AB是⊙O的直径,根据直径所对的圆周角是直角,可得∠ACB=90°,又由⊙O的直径为8cm,∠B=30°,即可求得答案;
(2)首先连接OD,由CD是∠ACB的角平分线,可求得∠BAD的度数,继而求得答案.
【解答】解:(1)∵AB是⊙O的直径,
∴∠ACB=90°,
∵AB=8cm,∠B=30°,
∴AC=
 AB=4cm,
AB=4cm,
∴BC=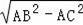
 =4
=4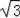
 cm;
cm;
(2)连接OD,
∵CD是∠ACB的角平分线,
∴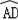
 =
=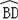
 ,
,
∴∠BOD=
 ∠AOB=90°,
∠AOB=90°,
∴∠BAD=
 ∠BOD=45°,
∠BOD=45°,
∵∠BAC=90°﹣∠B=60°,
∴∠CAD=∠BAC+∠BAD=105°.

【点评】此题考查了圆周角定理以及含30°角的直角三角形的性质.注意准确作出辅助线是解此题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
张师傅准备用长为8cm的铜丝剪成两段,以围成两个正方形的线圈,设剪成的两段铜丝中的一段的长为xcm,围成的两个正方形的面积之和为Scm2.
(1)求S与x的函数关系式,并写出自变量的取值范围;
(2)当x取何值时,S取得最小值,并求出这个最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
对于二次函数y=2(x﹣1)2﹣3的图象性质,下列说法不正确的是( )
A.开口向上 B.对称轴为直线x=1
C.顶点坐标为(1,﹣3) D.最小值为3
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知一次函数y=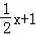
 的图象与x轴交于A点,与y轴交于B点:抛物线y=
的图象与x轴交于A点,与y轴交于B点:抛物线y=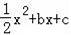
 的图象余一次函数y=
的图象余一次函数y=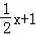
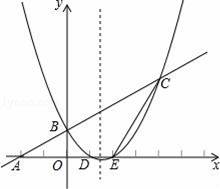
 的图象交于B、C两点,与x轴交于D、E两点,且点D的坐标为(1,0).
的图象交于B、C两点,与x轴交于D、E两点,且点D的坐标为(1,0).
(1)求点B的坐标;
(2)求该抛物线的解析式;
(3)求四边形BDEC的面积S;
(4)在x轴上是否存在点P,使得以点P、B、C为顶点的三角形是直角三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,过⊙O上一点C作⊙O的切线,交⊙O直径AB的延长线于点D.若∠D=40°,则∠A的度数为( )
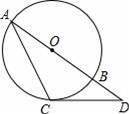

A.20° B.25° C.30° D.40°
查看答案和解析>>
科目:初中数学 来源: 题型:
某水果批发商场经销一种水果,如果每千克盈利5元,每天可售出200千克,经市场调查发现,在进价不变的情况下,若每千克涨价1元,销售量将减少10千克.
(1)现该商场要保证每天盈利1500元,同时又要顾客得到实惠,那么每千克应涨价多少元?
(2)若该商场单纯从经济利益角度考虑,这种水果每千克涨价多少元,能使商场获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
已知某实验区甲、乙品种水稻的平均产量相等,且甲、乙品种水稻产量的方差分别
为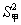 =79.6,
=79.6,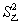 =68.5.由此可知
=68.5.由此可知 :在该地区____种水稻更具有推广价值.
:在该地区____种水稻更具有推广价值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com