
���� ��1����ˮ�����ٶ�Ϊxǧ��/ʱ�����ִ��ھ�ˮ�е��ٶ�Ϊ��x+15��ǧ��/ʱ������ʱ����з��̵�$\frac{150}{x+15+x}$=$\frac{150}{x+15-x}$-4��Ȼ��ⷽ�̣��ٽ��м���õ�x��ֵ���ɣ�
��2�������ٶȹ�ʽ�õ�t1=$\frac{150}{v+u}$+$\frac{150}{v-u}$=$\frac{300}{��v-u����v+u��}$•v��t2=$\frac{300}{v}$��Ȼ���������Ƚϴ�С���ɣ�
��� �⣺��1����ˮ�����ٶ�Ϊxǧ��/ʱ�����ִ��ھ�ˮ�е��ٶ�Ϊ��x+15��ǧ��/ʱ��
���������$\frac{150}{x+15+x}$=$\frac{150}{x+15-x}$-4�����x=5��������x=5��ԭ���̵Ľ⣬
��ˮ�����ٶ�Ϊ5ǧ��/ʱ��
��2��t1=$\frac{150}{v+u}$+$\frac{150}{v-u}$=$\frac{300}{��v-u����v+u��}$•v��t2=$\frac{300}{v}$��
t1-t2=$\frac{300}{��v-u����v+u��}$•v-$\frac{300}{v}$=$\frac{300}{v��v-u����v-u��}$[v2-��v-u����v-u��]=$\frac{300}{v��v-u����v-u��}$•u2��
��Ϊu��0��
����t1-t2��0��
��t1��t2��
���� ���⿼�����д���ʽ�����������������йصĴ���ú������֡���ĸ��������ŵ�ʽ�ӱ�ʾ�����������д���ʽ�� �������Ĺؼ��DZ�ʾ�ִ�˳ˮ����ˮ�е��ٶȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
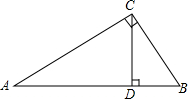 ��ͼ��Rt��ABC�У�CD��б��AB�ϵĸߣ���֤��
��ͼ��Rt��ABC�У�CD��б��AB�ϵĸߣ���֤���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com