
【题目】七(1)班同学为了解2018年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,请解答以下问题:

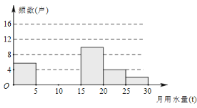
(1)求![]() ,
,![]() 的值.并把频数直方图补充完整;
的值.并把频数直方图补充完整;
(2)求该小区用水量不超过![]() 的家庭占被调在家庭总数的百分比;
的家庭占被调在家庭总数的百分比;
(3)若该小区有1000户家庭,根据调查数据估计,该小区月均用水是超过![]() 的家庭大约有多少户?
的家庭大约有多少户?
【答案】(1)![]() ,
,![]() ,图详见解析;(2)
,图详见解析;(2)![]() ;(3)120.
;(3)120.
【解析】
(1)根据![]() 中频数为
中频数为![]() ,频率为
,频率为![]() ,则调查总户数为
,则调查总户数为![]() ,进而得出在
,进而得出在![]() 范围内的频数以及在
范围内的频数以及在![]() 范围内的频率;由频数分布表中的数据补全直方图即可;
范围内的频率;由频数分布表中的数据补全直方图即可;
(2)根据(1)中所求即可得出不超过![]() 的家庭总数即可求出,不超过
的家庭总数即可求出,不超过![]() 的家庭占被调查家庭总数的百分比;
的家庭占被调查家庭总数的百分比;
(3)根据样本数据中超过![]() 的家庭数,即可得出
的家庭数,即可得出![]() 户家庭超过
户家庭超过![]() 的家庭数.
的家庭数.
解:(1)∵调查的家庭总数是:![]() 户
户
∴月用电量![]() 的户数是:
的户数是:![]() 户;月用电量
户;月用电量![]() 所占的比例是:
所占的比例是:![]() ;
;
频数分布直方图如下:
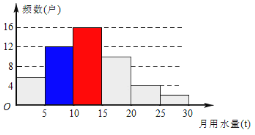 ;
;
(2)![]()
答:该小区用水量不超过![]() 的家庭占被调查家庭总数的百分比是
的家庭占被调查家庭总数的百分比是![]() .
.
(3)![]() 户
户
答:该小区月均用水量超过![]() 的家庭大约有
的家庭大约有![]() 户.
户.
故答案是:(1)![]() ,
,![]() ,图详见解析;(2)
,图详见解析;(2)![]() ;(3)
;(3)![]()


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
【题目】某校为了解“阳光体育”活动的开展情况,从全校1000名学生中,随机抽取部分学生进行问卷调查(每名学生只能从A、B、C、D中选择一项自己喜欢的活动项目),并将调查结果绘制成如下两幅不完整的统计图.



A:踢毽子 B:乒乓球 C:篮球 D:跳绳
根据以上信息,解答下列问题:
(1)被调查的学生共有 人,并补全条形统计图;
(2)在扇形统计图中,求表示区域D的扇形圆心角的度数;
(3)全校学生中喜欢篮球的人数大约是多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2+bx+c的图象经过点A(-1,12),B(2,-3).
(1)求这个二次函数的解析式;
(2)求这个图象的顶点坐标及与x轴的交点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个数能表示成某个整数的平方的形式,则称这个数为完全平方数,完全平方数是非负数.例如:0=02,1=12,4=22,9=32,16=42,25=52,36=62,121=112….
(1)若28+210+2n是完全平方数,求n的值.
(2)若一个正整数,它加上61是一个完全平方数,当减去11是另一个完全平方数,写出所有符合的正整数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD的顶点为A(1,2),B(﹣1,2),C(﹣1,﹣2),D(1,﹣2).点M和点N同时从E点出发,沿四边形的边做环绕匀速运动,M点以1单位/s的速度做逆时针运动,N点以2单位/s的速度做顺时针运动,则点M和点N第2016次相遇时的坐标为_____.
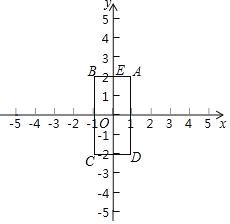
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.
(1)求证:AC是⊙O的切线;
(2)若BF=6,⊙O的半径为5,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE;②BC=DE;③∠C=∠D;④∠B=∠E,其中能使△ABC≌△AED的条件是______________.(填写序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)课本习题回放:如图①,∠ACB=90°,AC=BC, AD⊥CE,BE⊥CE,垂足分别为D,E,AD=2.5cm,DE=1.7cm..求BE的长.
(2)探索证明:如图②,点B、C在∠MAN的边AM、AN上,点E, F在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,∠1=∠2=∠BAC.求证:△ABE≌△CAF.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com