
【题目】(1)课本习题回放:如图①,∠ACB=90°,AC=BC, AD⊥CE,BE⊥CE,垂足分别为D,E,AD=2.5cm,DE=1.7cm..求BE的长.
(2)探索证明:如图②,点B、C在∠MAN的边AM、AN上,点E, F在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,∠1=∠2=∠BAC.求证:△ABE≌△CAF.

【答案】(1)0.8cm;(2)见解析
【解析】
(1)利用AAS定理证明△CEB≌△ADC,根据全等三角形的性质、结合图形解答即可;
(2)根据等角的补角相等得到∠BEA=∠AFC,根据三角形的外角的性质证明∠ABE=∠4,再利用AAS定理证明即可.
(1)∵BE⊥CE,AD⊥CE,∴∠E=∠ADC=90°,∴∠EBC+∠BCE=90°.
∵∠BCE+∠ACD=90°,∴∠EBC=∠DCA.
在△CEB和△ADC中,∵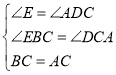 ,∴△CEB≌△ADC(AAS),∴BE=DC,CE=AD=2.5.
,∴△CEB≌△ADC(AAS),∴BE=DC,CE=AD=2.5.
∵DC=CE﹣DE,DE=1.7,∴DC=2.5﹣1.7=0.8,∴BE=0.8(cm);
(2)∵∠1=∠2,∴∠BEA=∠AFC.
∵∠1=∠ABE+∠3,∠3+∠4=∠BAC,∠1=∠BAC,∴∠BAC=∠ABE+∠3 ∴∠4=∠ABE.
∵∠BEA =∠AFC,∠ABE=∠4,AB=AC,∴△ABE≌△CAF(AAS)


 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:
【题目】七(1)班同学为了解2018年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,请解答以下问题:

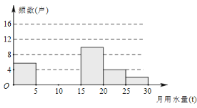
(1)求![]() ,
,![]() 的值.并把频数直方图补充完整;
的值.并把频数直方图补充完整;
(2)求该小区用水量不超过![]() 的家庭占被调在家庭总数的百分比;
的家庭占被调在家庭总数的百分比;
(3)若该小区有1000户家庭,根据调查数据估计,该小区月均用水是超过![]() 的家庭大约有多少户?
的家庭大约有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
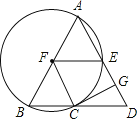
【题目】如图,在![]() 中,
中,![]() ,以AB为直径的
,以AB为直径的![]() 交BD于点C,交AD于点E,
交BD于点C,交AD于点E,![]() 于点G,连接FE,FC.
于点G,连接FE,FC.
![]() 求证:GC是
求证:GC是![]() 的切线;
的切线;
![]() 填空:
填空:
![]() 若
若![]() ,
,![]() ,则
,则![]() 的面积为______.
的面积为______.
![]() 当
当![]() 的度数为______时,四边形EFCD是菱形.
的度数为______时,四边形EFCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC≌△A′B′C,∠ACB=90°,∠B=50°,点B′在线段AB上,AC,A′B′交于点O,则∠COA′的度数是( )

A.50°B.60°
C.45°D.80°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,∠MON=30°,点A1、A2、A3在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=a,则△A7B7A8的边长为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
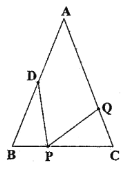
【题目】如图,在![]() 中,
中,![]() 厘米,
厘米,![]() 厘米,点
厘米,点![]() 为
为![]() 的中点.
的中点.
(1)如果点![]() 在线段
在线段![]() 上以
上以![]() 厘米
厘米![]() 秒的速度由
秒的速度由![]() 向
向![]() 点运动,同时点
点运动,同时点![]() 在线段
在线段![]() 上由
上由![]() 点向
点向![]() 点运动.
点运动.
①若点![]() 的运动速度与点
的运动速度与点![]() 的运动速度相等,
的运动速度相等,![]() 秒钟时,
秒钟时,![]() 与
与![]() 是否全等?请说明理由;
是否全等?请说明理由;
②点![]() 的运动速度与点
的运动速度与点![]() 的运动速度不相等,当点
的运动速度不相等,当点![]() 的运动速度为多少时,能够使
的运动速度为多少时,能够使![]() ?并说明理由;
?并说明理由;
(2)若点![]() 以②中的运动速度从点
以②中的运动速度从点![]() 出发,点
出发,点![]() 以原来运动速度从点
以原来运动速度从点![]() 同时出发,都逆时针沿
同时出发,都逆时针沿![]() 的三边运动,求多长时间点
的三边运动,求多长时间点![]() 与点
与点![]() 第一次在
第一次在![]() 的哪条边上相遇?
的哪条边上相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
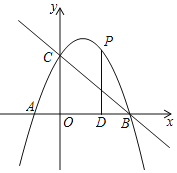
【题目】如图,抛物线![]() 与坐标轴交点分别为
与坐标轴交点分别为![]() ,
,![]() ,
,![]() ,作直线BC.
,作直线BC.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 点P为抛物线上第一象限内一动点,过点P作
点P为抛物线上第一象限内一动点,过点P作![]() 轴于点D,设点P的横坐标为
轴于点D,设点P的横坐标为![]() ,求
,求![]() 的面积S与t的函数关系式;
的面积S与t的函数关系式;
![]() 条件同
条件同![]() ,若
,若![]() 与
与![]() 相似,求点P的坐标.
相似,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:AP平分![]() ,点B是射线AP上一定点,点C在直线AM上运动,连接BC.
,点B是射线AP上一定点,点C在直线AM上运动,连接BC.
![]() 如图1,
如图1,![]() ,将
,将![]() 的两边射线BC和BA分别绕点B顺时针旋转
的两边射线BC和BA分别绕点B顺时针旋转![]() ,旋转后角的两边分别与射线AN交于点D和点
,旋转后角的两边分别与射线AN交于点D和点![]() 当点C在射线AM上时,请直接写出:
当点C在射线AM上时,请直接写出:
![]() 和BC之间的数量关系是______;
和BC之间的数量关系是______;
![]() 线段AC,AD和AB之间的数量关系是______.
线段AC,AD和AB之间的数量关系是______.
![]() 如果
如果![]() ,将
,将![]() 的两边射线BC和BA分别绕点B顺时针旋转
的两边射线BC和BA分别绕点B顺时针旋转![]() ,旋转后角的两边分别与射线AN交于点D和点E.
,旋转后角的两边分别与射线AN交于点D和点E.
![]() 如图2,当点C在射线AM上时,请探究线段AC,AD和AB之间的数量关系,写出结论并给予证明;
如图2,当点C在射线AM上时,请探究线段AC,AD和AB之间的数量关系,写出结论并给予证明;
![]() 如图3,当点C在射线AM的反向延长线上时,BC交射线AN于点F,若
如图3,当点C在射线AM的反向延长线上时,BC交射线AN于点F,若![]() ,
,![]() ,请直接写出线段AD和DF的长.
,请直接写出线段AD和DF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校英语社团举行了“单词听写大赛”,每位参赛选手共听写单词100个![]() 现从参加比赛的男女选手中分别随机抽取部分学生进行调查,对答对的情况进行分组如下:组:
现从参加比赛的男女选手中分别随机抽取部分学生进行调查,对答对的情况进行分组如下:组:![]() ,B组:
,B组:![]() ,C组:
,C组:![]() ,D组:
,D组:![]() ,E组:
,E组:![]() 并绘制了如下不完整的统计图:
并绘制了如下不完整的统计图:

请根据以上信息解答下列问题:
![]() 本次调查共抽取了多少名学生,并将条形统计图补充完整;
本次调查共抽取了多少名学生,并将条形统计图补充完整;
![]() 求出A组所对的扇形圆心角的度数;
求出A组所对的扇形圆心角的度数;
![]() 若从D、E两组中分别抽取一位学生进行采访,请用画树状图或列表法求出恰好抽到两位女学生的概率.
若从D、E两组中分别抽取一位学生进行采访,请用画树状图或列表法求出恰好抽到两位女学生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com