
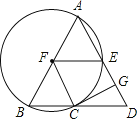
【题目】如图,在![]() 中,
中,![]() ,以AB为直径的
,以AB为直径的![]() 交BD于点C,交AD于点E,
交BD于点C,交AD于点E,![]() 于点G,连接FE,FC.
于点G,连接FE,FC.
![]() 求证:GC是
求证:GC是![]() 的切线;
的切线;
![]() 填空:
填空:
![]() 若
若![]() ,
,![]() ,则
,则![]() 的面积为______.
的面积为______.
![]() 当
当![]() 的度数为______时,四边形EFCD是菱形.
的度数为______时,四边形EFCD是菱形.
【答案】![]()
![]()
【解析】
(1)由等腰三角形的性质得出∠D=∠BCF,证出CF∥AD,由已知条件得出CG⊥CF,即可得出结论;
(2)解:①连接AC,BE,根据圆周角定理得到AC⊥BD,∠AEB=90°,根据等腰三角形的性质得到BC=CD,解直角三角形得到DE=2![]() -2,根据三角形的中位线的性质得到DG=EG=
-2,根据三角形的中位线的性质得到DG=EG=![]() DE=
DE=![]() -1,CG=
-1,CG=![]() BE=1,于是得到结论;
BE=1,于是得到结论;
②证出△BCF是等边三角形,得出∠B=60°,CF=BF=![]() AB,证出△ABD是等边三角形,CF=
AB,证出△ABD是等边三角形,CF=![]() AD,证出△AEF是等边三角形,得出AE=AF=
AD,证出△AEF是等边三角形,得出AE=AF=![]() AB=
AB=![]() AD,因此CF=DE,证出四边形EFCD是平行四边形,即可得出结论.
AD,因此CF=DE,证出四边形EFCD是平行四边形,即可得出结论.
![]() 证明:
证明:![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 是
是![]() 的切线;
的切线;
![]() 解:
解:![]() 连接AC,BE,
连接AC,BE,
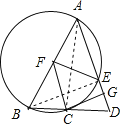
![]() 是
是![]() 的直径,
的直径,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() 的面积
的面积![]() ;
;
故答案为:![]() ;
;
![]() 当
当![]() 的度数为
的度数为![]() 时,四边形EFCD是菱形
时,四边形EFCD是菱形![]() 理由如下:
理由如下:
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() ,
,![]() ,
,
![]() ,
,
![]() 是等边三角形,
是等边三角形,![]() ,
,
![]() ,
,
![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() ,
,
![]() ,
,
又![]() ,
,
![]() 四边形EFCD是平行四边形,
四边形EFCD是平行四边形,
![]() ,
,
![]() 四边形EFCD是菱形;
四边形EFCD是菱形;
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.
(1)求证:AC是⊙O的切线;
(2)若BF=6,⊙O的半径为5,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE;②BC=DE;③∠C=∠D;④∠B=∠E,其中能使△ABC≌△AED的条件是______________.(填写序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】红旗镇镇政府大力发动农户扩大柑橘和蔬菜种植面积,取得了较好的经济效益.今年红旗镇柑橘和蔬菜的收成比去年一共增加了80吨,其中柑橘的收成比去年增加了20%,蔬菜的收成比去年增加了30%,从而使今年的收成共达到420吨.
(1)红旗镇去年柑橘和蔬菜的收成各多少吨?
(2)由于今年大丰收,红旗镇政府计划用甲、乙两种货车共33辆将柑橘和蔬菜全部一次性运到外地去销售.已知一辆甲种货车最多可装13吨柑橘和3吨蔬菜;一辆乙种货车最多可装柑橘和蔬菜各6吨,安排甲、乙两种货车共有几种方案?
(3)若甲种货车的运费为每辆600元,乙种货车的运费为每辆500元,在(2)的情况下,如何安排运费最少,最少为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.

(1)求证:DE=DF;
(2)若∠A=60°,BE=1,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=![]() x-3与反比例函数y=
x-3与反比例函数y=![]() 的图象相交于点A(4,n),与x轴相交于点B.
的图象相交于点A(4,n),与x轴相交于点B.

(1)填空:n的值为 ,k的值为 ;
(2)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;
(3)观察反比函数y=![]() 的图象,当y≥-2时,请直接写出自变量x的取值范围.
的图象,当y≥-2时,请直接写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)课本习题回放:如图①,∠ACB=90°,AC=BC, AD⊥CE,BE⊥CE,垂足分别为D,E,AD=2.5cm,DE=1.7cm..求BE的长.
(2)探索证明:如图②,点B、C在∠MAN的边AM、AN上,点E, F在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,∠1=∠2=∠BAC.求证:△ABE≌△CAF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】兴隆商场用36万元购进A、B两种品牌的服装,销售完后共获利6万元,其进价和售价如下表:

该商场购进A、B两种服装各多少件?
(2)第二次以原价购进A、B两种服装,购进B服装的件数不变,购进A服装的件数是第一次的2倍,A种服装按原价出售,而B种服装打折销售;若两种服装销售完毕,要使第二次销售活动获利不少于81600元,则B种服装最低打几折销售?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com