
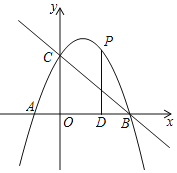
【题目】如图,抛物线![]() 与坐标轴交点分别为
与坐标轴交点分别为![]() ,
,![]() ,
,![]() ,作直线BC.
,作直线BC.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 点P为抛物线上第一象限内一动点,过点P作
点P为抛物线上第一象限内一动点,过点P作![]() 轴于点D,设点P的横坐标为
轴于点D,设点P的横坐标为![]() ,求
,求![]() 的面积S与t的函数关系式;
的面积S与t的函数关系式;
![]() 条件同
条件同![]() ,若
,若![]() 与
与![]() 相似,求点P的坐标.
相似,求点P的坐标.
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.
(1)求证:AC是⊙O的切线;
(2)若BF=6,⊙O的半径为5,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=![]() x-3与反比例函数y=
x-3与反比例函数y=![]() 的图象相交于点A(4,n),与x轴相交于点B.
的图象相交于点A(4,n),与x轴相交于点B.

(1)填空:n的值为 ,k的值为 ;
(2)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;
(3)观察反比函数y=![]() 的图象,当y≥-2时,请直接写出自变量x的取值范围.
的图象,当y≥-2时,请直接写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)课本习题回放:如图①,∠ACB=90°,AC=BC, AD⊥CE,BE⊥CE,垂足分别为D,E,AD=2.5cm,DE=1.7cm..求BE的长.
(2)探索证明:如图②,点B、C在∠MAN的边AM、AN上,点E, F在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,∠1=∠2=∠BAC.求证:△ABE≌△CAF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】养牛场原有大牛30头和小牛15头,一天约用饲料675kg.一周后又购进12头大牛和5头小牛,这时1天约用饲料940kg.饲养员李大叔估计每头大牛1天约需饲料1820kg,每头小牛1天约需饲料78kg,你能通过计算检验他的估计吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解“阳光体育”活动情况,我市教育部门在某所初中2000名学生中,随机抽取了若干学生进行问卷调查(要求每位学生只能填写一种自己喜欢的活动),并将调查的结果绘制成如图的两个不完整的统计图:
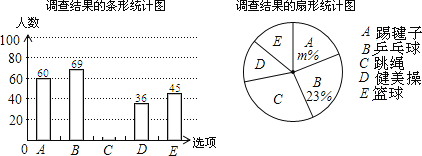
根据以上信息解答下列问题:
(1)参加调查的人数共有_____人,在扇形图中,表示“C”的扇形的圆心角为______度;
(2)补全条形统计图,并计算扇形统计图中的m;
(3)估计该校喜欢“B”项目的学生一共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=90°,点D为线段BC上的一个动点,以AD为直角边向右作等腰Rt△ADF,使AD=AF,∠DAF=90°.
(1)如图1,连结CF,求证:△ABD≌△ACF;
(2)如图2,过A点作△ADF的对称轴交BC于点E,猜想BD2,DE2,CE2关系,并证明你的结论;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】兴隆商场用36万元购进A、B两种品牌的服装,销售完后共获利6万元,其进价和售价如下表:

该商场购进A、B两种服装各多少件?
(2)第二次以原价购进A、B两种服装,购进B服装的件数不变,购进A服装的件数是第一次的2倍,A种服装按原价出售,而B种服装打折销售;若两种服装销售完毕,要使第二次销售活动获利不少于81600元,则B种服装最低打几折销售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB丄CD于点E,且AB = CD = AC,若点I是三角形ACE的角平分线的交点,点F是BD的中点.下列结论:①∠AIC= 135°;②BD = BI,③S△AIC = S△BID ;④IF⊥AC.其中正确的是_________(填序号).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com