
����Ŀ����֪��APƽ��![]() ����B������AP��һ���㣬��C��ֱ��AM���˶�������BC��
����B������AP��һ���㣬��C��ֱ��AM���˶�������BC��
![]() ��ͼ1��
��ͼ1��![]() ����
����![]() ����������BC��BA�ֱ��Ƶ�B˳ʱ����ת
����������BC��BA�ֱ��Ƶ�B˳ʱ����ת![]() ����ת��ǵ����߷ֱ�������AN���ڵ�D�͵�
����ת��ǵ����߷ֱ�������AN���ڵ�D�͵�![]() ����C������AM��ʱ����ֱ��д����
����C������AM��ʱ����ֱ��д����
![]() ��BC֮���������ϵ��______��
��BC֮���������ϵ��______��
![]() �߶�AC��AD��AB֮���������ϵ��______��
�߶�AC��AD��AB֮���������ϵ��______��
![]() ���
���![]() ����
����![]() ����������BC��BA�ֱ��Ƶ�B˳ʱ����ת
����������BC��BA�ֱ��Ƶ�B˳ʱ����ת![]() ����ת��ǵ����߷ֱ�������AN���ڵ�D�͵�E��
����ת��ǵ����߷ֱ�������AN���ڵ�D�͵�E��
![]() ��ͼ2������C������AM��ʱ����̽���߶�AC��AD��AB֮���������ϵ��д�����۲�����֤����
��ͼ2������C������AM��ʱ����̽���߶�AC��AD��AB֮���������ϵ��д�����۲�����֤����
![]() ��ͼ3������C������AM�ķ����ӳ�����ʱ��BC������AN�ڵ�F����
��ͼ3������C������AM�ķ����ӳ�����ʱ��BC������AN�ڵ�F����![]() ��
��![]() ����ֱ��д���߶�AD��DF�ij���
����ֱ��д���߶�AD��DF�ij���

���𰸡�![]() ��
��![]() ��
��![]() ��
��![]() ��֤����������
��֤����������![]() ��
��![]() ��
��
��������
![]() ���жϳ�
���жϳ�![]() �������ó�
�������ó�![]() ���жϳ�
���жϳ�![]() ��
��![]() �����ɵó����ۣ�
�����ɵó����ۣ�
![]() ���жϳ��ı���AGBH�������Σ������ó�
���жϳ��ı���AGBH�������Σ������ó�![]() �����жϳ�
�����жϳ�![]() �����ɵó����ۣ�
�����ɵó����ۣ�
![]() ͬ
ͬ![]() �ķ������ɵó����ۣ�
�ķ������ɵó����ۣ�
![]() ��ͼ3�У���
��ͼ3�У���![]() ��G��
��G��![]() ��H��
��H��![]() ��
��![]() ��
��![]() ��֪��
��֪��![]() ��
��![]() ��
��![]() ��
��![]() ����֪
����֪![]() ��
��![]() ��
��![]() ���Ƴ�
���Ƴ�![]() ����
����![]() ���ɵ�
���ɵ�![]() ����
����![]() ����
����![]() ��
��![]() ����
����![]() ��
��![]() ���ɵ�
���ɵ�![]() �����y���ɽ�����⣮
�����y���ɽ�����⣮
![]() ��ͼ1��
��ͼ1��
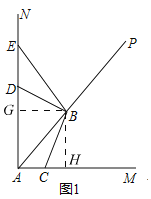
����B��![]() ��G��
��G��![]() ��H��
��H��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��![]() ��ƽ���ߣ�
��ƽ���ߣ�![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
�ʴ�Ϊ![]() ��
��
![]() ��ͼ1����
��ͼ1����![]() ֪������B��
֪������B��![]() ��G��
��G��![]() ��H��
��H��
![]() ��
��
![]() �ı���AGBH�Ǿ��Σ�
�ı���AGBH�Ǿ��Σ�
��![]() ֪��
֪��![]() ��
��
![]() ����AGBH��������
����AGBH��������
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
�ʴ�Ϊ��![]() ��
��
![]() ��ͼ2��
��ͼ2��
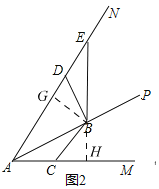
����B��![]() ��G��
��G��![]() ��H��
��H��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��![]() ��ƽ���ߣ�
��ƽ���ߣ�![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��![]() ��ƽ���ߣ�
��ƽ���ߣ�
![]() ��
��
��![]() ��
��![]() ��
��
![]() ��
��
![]() ��ͼ3�У�
��ͼ3�У�
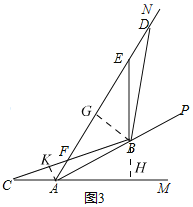
��![]() ��G��
��G��![]() ��H��
��H��![]() ��K��
��K��
��![]() ��֪��
��֪��![]() ��
��![]() ��
��
��֤��![]() ��
��![]() ��
��
��֪![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
��![]() ����
����![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
����ƽ���������ã�![]() ��
��
���![]() ��
��![]() ����AC����ȥ
����AC����ȥ![]()
![]() ��
��
����![]() ��
��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��1=��2��AC=AD������������������AB=AE����BC=DE���ۡ�C=��D���ܡ�B=��E��������ʹ��ABC�ա�AED��������______________������д��ţ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1���α�ϰ��طţ���ͼ��,��ACB=90��,AC=BC, AD��CE,BE��CE,����ֱ�ΪD,E��AD=2.5cm��DE=1.7cm..��BE�ij�.
��2��̽��֤������ͼ�ڣ���B��C�ڡ�MAN�ı�AM��AN�ϣ���E, F�ڡ�MAN�ڲ�������AD�ϣ���1����2�ֱ�����ABE����CAF����ǣ���֪AB=AC,��1=��2=��BAC.��֤����ABE�ա�CAF.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽⡰�������������������н���������ij������2000��ѧ���У������ȡ������ѧ�������ʾ����飨Ҫ��ÿλѧ��ֻ����дһ���Լ�ϲ���Ļ������������Ľ�����Ƴ���ͼ��������������ͳ��ͼ��
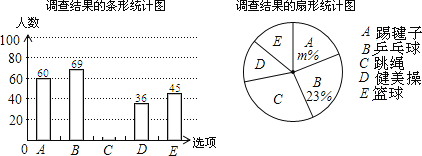
����������Ϣ����������⣺
��1���μӵ������������_____�ˣ�������ͼ�У���ʾ��C�������ε�Բ�Ľ�Ϊ______�ȣ�
��2����ȫ����ͳ��ͼ������������ͳ��ͼ�е�m��
��3�����Ƹ�Уϲ����B����Ŀ��ѧ��һ���ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У�AB=AC����BAC=90������DΪ�߶�BC�ϵ�һ�����㣬��ADΪֱ�DZ�����������Rt��ADF��ʹAD=AF����DAF=90����
��1����ͼ1������CF����֤����ABD�ա�ACF��
��2����ͼ2����A������ADF�ĶԳ��ύBC�ڵ�E������BD2��DE2��CE2��ϵ����֤����Ľ��ۣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y��2x2��8x+m������������������2��x����1ʱ������ͼ��λ��x����·�����6��x��7ʱ������ͼ��λ��x����Ϸ�����m��ֵΪ��������
A. 8 B. ��10 C. ��42 D. ��24
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����¡�̳���36��Ԫ����A��B����Ʒ�Ƶķ�װ�����������6��Ԫ������ۺ��ۼ����±���

���̳�����A��B���ַ�װ�����ټ���
��2���ڶ�����ԭ�۹���A��B���ַ�װ������B��װ�ļ������䣬����A��װ�ļ����ǵ�һ�ε�2����A�ַ�װ��ԭ�۳��ۣ���B�ַ�װ�������ۣ������ַ�װ������ϣ�Ҫʹ�ڶ������ۻ����������81600Ԫ����B�ַ�װ��ʹ������ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪B��E��C��F��ͬһ��ֱ���ϣ�BE��CF��AB��DE�������������У������ж���ABC�ա�DEF����(����)

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУ��֯![]() ��ͬѧ��
��ͬѧ��![]() ����ʦ�μ�У��ѧϰ������ִ���ѡ���С���ֿͳ�����ͳ��ؿ���Ϊ
����ʦ�μ�У��ѧϰ������ִ���ѡ���С���ֿͳ�����ͳ��ؿ���Ϊ![]() ��/����С�ͳ��ؿ���Ϊ
��/����С�ͳ��ؿ���Ϊ![]() ��/��
��/��
��1��ѧУ������![]() ���ͳ����м��������?
���ͳ����м��������?
��2���ڣ�1���������£�����ͳ����Ϊ![]() Ԫ/����С�ͳ����Ϊ
Ԫ/����С�ͳ����Ϊ![]() Ԫ/���������������ʡǮ?
Ԫ/���������������ʡǮ?
��3��ѧУ��ʱ����![]() ��ѧ����
��ѧ����![]() ����ʦ�μӻ��ÿ����ͳ���2����ʦ���ӣ�ÿ��С�ͳ�������
����ʦ�μӻ��ÿ����ͳ���2����ʦ���ӣ�ÿ��С�ͳ�������![]() ����ʦ����.ͬѧ��������ͳ�������������С�ͳ������һ��С�ͳ�����Ҫ��
����ʦ����.ͬѧ��������ͳ�������������С�ͳ������һ��С�ͳ�����Ҫ��![]() �ˣ����������������
�ˣ����������������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com