
���� ������ÿ̨A�͵��Ժ�B�͵��Ե���������ֱ�ΪxԪ��yԪ���г������鼴�ɽ�����⣮
���ٸ���������=A������+B�������ɽ�����⣮
������Ա���xȡֵ��Χ������һ�κ��������Խ����
��� �⣺������ÿ̨A�͵��Ժ�B�͵��Ե���������ֱ�ΪxԪ��yԪ��
������$\left\{\begin{array}{l}{x+3y=550}\\{2x+3y=650}\end{array}\right.$���$\left\{\begin{array}{l}{x=100}\\{y=150}\end{array}\right.$��
��ÿ̨A�͵��Ժ�B�͵��Ե���������ֱ�Ϊ100Ԫ��150Ԫ��
����y=100x+150��100-x��=-50x+15000��
100-x��2x��
x��$\frac{100}{3}$��
��x��34��x����������
�ڡ�y=-50x+15000��
k=-50��0��
��y��x���������
��x=34ʱ��y���ֵ=14830��
��A��34̨��B��66̨ʱ�������������
���� ���⿼��һ�κ�����Ӧ�ã����������֪ʶ������Ĺؼ��ǹ���һ�κ���������һ�κ��������ʽ�����⣬�����п��������ͣ�


 ��ҵ����ϵ�д�
��ҵ����ϵ�д� ͬ��ѧ��һ�ζ���ϵ�д�
ͬ��ѧ��һ�ζ���ϵ�д� �����ܾ�ϵ�д�
�����ܾ�ϵ�д� ���ƿ�����ϵ�д�
���ƿ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1��2�� | B�� | ��2��-1�� | C�� | ��-2��1�� | D�� | ��-2��-1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | M��N | B�� | M=N | C�� | M��N | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
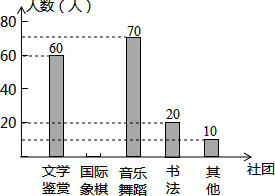 Ϊ����γ̸ĸijУ������չУ���γ̽��裬�ƻ���������ѧ���͡������������塱���������赸���͡��鷨���ȶ�����ţ�Ҫ��ÿλѧ��������ѡ������һ�����ţ�Ϊ�ˣ���������˱�У����ѧ��ѡ�����ŵ����������������Ƴ�����ͳ��ͼ��������������
Ϊ����γ̸ĸijУ������չУ���γ̽��裬�ƻ���������ѧ���͡������������塱���������赸���͡��鷨���ȶ�����ţ�Ҫ��ÿλѧ��������ѡ������һ�����ţ�Ϊ�ˣ���������˱�У����ѧ��ѡ�����ŵ����������������Ƴ�����ͳ��ͼ��������������| ѡ������ | ��ѧ���� | �������� | �����赸 | �鷨 | ���� |
| ��ռ�ٷֱ� | a | 20% | b | 10% | 5% |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У���B=60�㣬AB��AC=5��7��������Բ��O��BC��AC��AB�ֱ����ڵ�D��E��F���ҡ�O�����Ϊ12�У����ABC�����߳���
��ͼ���ڡ�ABC�У���B=60�㣬AB��AC=5��7��������Բ��O��BC��AC��AB�ֱ����ڵ�D��E��F���ҡ�O�����Ϊ12�У����ABC�����߳����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ������ABC���Ź�AB�е�D��ֱ���۵���ʹ��A����BC���ϵ�A1�����ۺ���AC�߽��ڵ�E���ֱ����D��E��BC�Ĵ��ߣ�����ΪQ��P����Ϊ��1�β��������ı���DEPQ�����ΪS1����ԭֽƬ���ٽ���ADE���Ź�AD�е�D1��ֱ���۵���ʹ��A����DE���ϵ�A2�����ۺ���AC�߽��ڵ�E1���ֱ����D1��E1��BC�Ĵ��ߣ�����ΪQ1��P1����Ϊ��2�β��������ı���D1E1P1Q1�����ΪS2���������������ϲ�����ȥ��������ABC�����Ϊ1����Sn��ֵΪ��������
��ͼ������ABC���Ź�AB�е�D��ֱ���۵���ʹ��A����BC���ϵ�A1�����ۺ���AC�߽��ڵ�E���ֱ����D��E��BC�Ĵ��ߣ�����ΪQ��P����Ϊ��1�β��������ı���DEPQ�����ΪS1����ԭֽƬ���ٽ���ADE���Ź�AD�е�D1��ֱ���۵���ʹ��A����DE���ϵ�A2�����ۺ���AC�߽��ڵ�E1���ֱ����D1��E1��BC�Ĵ��ߣ�����ΪQ1��P1����Ϊ��2�β��������ı���D1E1P1Q1�����ΪS2���������������ϲ�����ȥ��������ABC�����Ϊ1����Sn��ֵΪ��������| A�� | $\frac{{2}^{2n}-2}{{2}^{2n}}$ | B�� | $\frac{{2}^{n}-1}{{2}^{2n-1}}$ | C�� | $\frac{{3}^{n}-1}{{2}^{2n}}$ | D�� | $\frac{{2}^{n-1}-1}{{2}^{2n}}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3.89 | B�� | 3.9 | C�� | 3.90 | D�� | 3.896 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��1 | B�� | x��3 | C�� | x��1��x��3 | D�� | x��3��x��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ѧϰ����ͼʱ����ʦ�ڽ�̨�����ĺз۱ʺаڷų���ͼ��״�ļ����壬��ô�ü����������ͼ��ȷ���ǣ�������
��ѧϰ����ͼʱ����ʦ�ڽ�̨�����ĺз۱ʺаڷų���ͼ��״�ļ����壬��ô�ü����������ͼ��ȷ���ǣ�������| A�� | 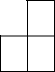 | B�� | 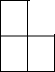 | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com