
 如图,在△ABC中,∠B=60°,AB:AC=5:7,其内切圆⊙O与BC、AC、AB分别切于点D、E、F,且⊙O的面积为12π,求△ABC的三边长.
如图,在△ABC中,∠B=60°,AB:AC=5:7,其内切圆⊙O与BC、AC、AB分别切于点D、E、F,且⊙O的面积为12π,求△ABC的三边长. 分析 过点A作AH⊥BC于H,连接OA、OB、OC、OD、OE、OF,如图,根据条件可求出⊙O的半径,根据切线长定理可得BF=BD,CD=CE,AE=AF,∠FBO=∠DBO=30°,在Rt△ODB中运用三角函数可求出BD.设AB=5x,即可得到AC=7x,BC=2x+12,然后根据△ABC面积两种表示方法建立关于x的方程,求出x,即可解决问题.
解答 解:过点A作AH⊥BC于H,连接OA、OB、OC、OD、OE、OF,如图.
设AB=5x,由AB:AC=5:7得AC=7x.
∵S⊙O=πOD2=12π,∴OD=2$\sqrt{3}$,
∴OE=OF=OD=2$\sqrt{3}$.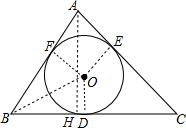
∵⊙O与BC、AC、AB分别切于点D、E、F,
∴BF=BD,CD=CE,AE=AF,∠FBO=∠DBO=$\frac{1}{2}$∠ABC=30°,
∴$\frac{OD}{BD}$=tan∠OBD=$\frac{\sqrt{3}}{3}$,
∴BD=$\sqrt{3}$OD=6,
∴BF=6,AE=AF=5x-6,
∴DC=EC=7x-(5x-6)=2x+6,
∴BC=6+2x+6=2x+12.
∵S△ABC=$\frac{1}{2}$BC•AH=$\frac{1}{2}$BC•AB•sin∠ABC=$\frac{1}{2}$(2x+12)•5x•$\frac{\sqrt{3}}{2}$=$\frac{5\sqrt{3}}{2}$x(x+6),
且S△ABC=S△OAB+S△OBC+S△OAC=$\frac{1}{2}$AB•OF+$\frac{1}{2}$BC•OD+$\frac{1}{2}$AC•OE
=$\frac{1}{2}$•2$\sqrt{3}$(AB+BC+AC)=$\sqrt{3}$(5x+2x+12+7x)=$\sqrt{3}$(14x+12),
∴$\frac{5\sqrt{3}}{2}$x(x+6)=$\sqrt{3}$(14x+12),
解得x1=2,x2=-$\frac{12}{5}$(舍去),
∴AB=5x=10,AC=7x=14,BC=2x+12=16.
点评 本题主要考查了切线长定理、三角函数、解一元二次方程、圆的面积公式、三角形的面积公式等知识,运用三角形面积两种表示建立方程是解决本题的关键.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
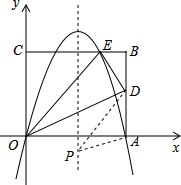 如图,矩形的边OA在x轴上,边OC在y轴上,点B的坐标为(10,8),沿直线OD折叠矩形,使点A正好落在BC上的E处,E点坐标为(6,8),抛物线y=ax2+bx+c经过O、A、E三点.
如图,矩形的边OA在x轴上,边OC在y轴上,点B的坐标为(10,8),沿直线OD折叠矩形,使点A正好落在BC上的E处,E点坐标为(6,8),抛物线y=ax2+bx+c经过O、A、E三点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x<1 | B. | x≥3 | C. | 1≤x<3 | D. | 1<x≤3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com