解:(1)∵△ABC和△ODC是等边三角形,
∴∠ABC=∠CAB=∠ODC=∠DOC=60°,BC=AC,CO=CD,∠ACB=∠DCO=60°,
∴∠ACB-∠ACO=∠DCO-∠ACO,
∴∠ACD=∠BCO,
在△BOC和△ADC中

,
∴△BOC≌△ADC(SAS);
(2)△AOD的形状是等边三角形
理由是:∵△BOC≌△ADC,∠BOC=α=120°,
∴∠ADC=∠BOC=120°,∠AOC=360°-120°-120°=120°,
∵∠ODC=∠DOC=60°,
∴∠ADO=∠AOD=60°,
∴AD=AO,
∴△AOD的形状是等边三角形;

(3)分为三种情况:①当∠ADO=90°时,α=150°,
理由是:∵∠BOC=∠ADC=α=150°,∠ODC=60°,
∴∠ADO=90°,
即△AOD是直角三角形;
②当∠AOD=90°时,α=90°,
理由是:∵∠AOC=360°-∠AOB-α=360°-90°-120°=150°,
∵∠DOC=60°,
∴∠AOD=90°,
∴△AOD是直角三角形;
③当∠OAD=90°时,∵△BOC≌△ADC,
∴∠CBO=∠DAC,
∵∠AOB=120°,
∴∠OAB+∠OBA=60°,
∵∠BAC=∠OAB+∠OAC=60°,
∴∠OAC=∠OBA,
∴∠DAO=∠OBA+∠OBC=∠ABC=60°,即∠OAD=90°此种情况不存在;
综合上述,当α等于150°或90°时,△AOD是直角三角形.
分析:(1)根据等边三角形性质得出∠ABC=∠CAB=∠ODC=∠DOC=60°,BC=AC,CO=CD,∠ACB=∠DCO=60°,求出∠ACD=∠BCO,根据SAS证出粮三角形全等即可;
(2)根据全等得出∠ADC=∠BOC=120°,求出∠AOC=120°,求出∠ADO=∠AOD=60°,根据等边三角形的判定推出即可;
(3)分为三种情况::①当∠ADO=90°时,α=150°,根据∠BOC=∠ADC=α=150°和∠ODC=60°求出∠ADO=90°即可;②当∠AOD=90°时,α=90°,求出∠AOC=150°,求出∠AOD=90°即可;③当∠OAD=90°时,求出∠DAO=∠ABC=60°不能等于90°此种情况不存在.
点评:本题考查了三角形的内角和定理,等边三角形的性质和判定,直角三角形的性质,全等三角形的性质和判定等知识点的综合运用.

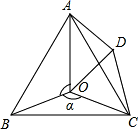 如图,点O是等边△ABC内一点,∠AOB=120°,∠BOC=α,△OCD也是等边三角形.
如图,点O是等边△ABC内一点,∠AOB=120°,∠BOC=α,△OCD也是等边三角形. ,
,


 21、如图,点D是等边三角形ABC内的一点,将△BDC绕点C顺时针旋转60°,试画出旋转后的三角形,并指出图中的全等图形以及它们的对应顶点、对应边和对应角.
21、如图,点D是等边三角形ABC内的一点,将△BDC绕点C顺时针旋转60°,试画出旋转后的三角形,并指出图中的全等图形以及它们的对应顶点、对应边和对应角. 21、如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=a.以OC为一边作等边三角形OCD,连接AC、AD.
21、如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=a.以OC为一边作等边三角形OCD,连接AC、AD. (2011•清流县质检)星期天,小明在解答下列题目时卡壳了.
(2011•清流县质检)星期天,小明在解答下列题目时卡壳了. 得到线段CD,连接OD、AD.
得到线段CD,连接OD、AD.