
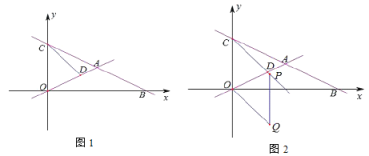
【题目】如图1,在平面直角坐标系中,直线![]() :
:![]() 与
与![]() :
:![]() 交于点
交于点![]() ,分别与
,分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() 、
、![]() .
.
(1)分别求出点![]() 、
、![]() 、
、![]() 的坐标;
的坐标;
(2)若![]() 是线段
是线段![]() 上的点,且
上的点,且![]() 的面积为12,求直线
的面积为12,求直线![]() 的函数表达式;
的函数表达式;
(3)在(2)的条件下,设![]() 是射线
是射线![]() 上的点.
上的点.
①如图2,过点![]() 作
作![]() ,且使四边形
,且使四边形![]() 为菱形,请直接写出点
为菱形,请直接写出点![]() 的坐标;
的坐标;
②在平面内是否存在其它点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?若存在,直接写出点
为顶点的四边形是菱形?若存在,直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)A(6,3).B(12,0).C(0,6),(2)y=x+6.(3)①Q(3![]() ,-3
,-3![]() ),②(3,3),(6,6).
),②(3,3),(6,6).
【解析】
(1)构建方程组确定交点A的坐标,利用待定系数法确定B,C两点坐标即可.
(2)设D(m,![]() m),利用三角形的面积公式,构建方程求出m的值,再利用待定系数法即可解决问题.
m),利用三角形的面积公式,构建方程求出m的值,再利用待定系数法即可解决问题.
(3)①构建OC=PC,设P(m,![]() m),利用两点间距离公式,构建方程求出m即可.
m),利用两点间距离公式,构建方程求出m即可.
②当OC为菱形的对角线时,OC垂直平分线段PQ,利用对称性解决问题即可;当PC为对角线时,OQ⊥CP, 利用对称性解决问题即可.
解:(1)由
解得![]()
∴A(6,3).
∵![]() 与分别与x轴、y轴交于点B、C,
与分别与x轴、y轴交于点B、C,
∴C(0,6),B(12,0).
(2)设D(m,![]() m),由题意:OC=6,△COD的面积为12,
m),由题意:OC=6,△COD的面积为12,
∴![]() ×6×m=12,
×6×m=12,
∴m=4,
∴D(4,2),∵C(0,6),
设直线CD的解析式为y=kx+b,
则有![]()
解得![]()
∴直线CD的解析式为y=x+6.
(3)①∵四边形OCPQ是菱形,
∴OC=PC=6,
设P(m,m+6),
∴m2+m2=36,
∴m=3![]() 或3
或3![]() ,
,
∴P(3![]() ,-3
,-3![]() +6),
+6),
∵PQ∥OC,PQ=OC,
![]() ,-3
,-3![]() )
)
②如图,当OC为菱形的对角线时,OC垂直平分线段PQ,
易知P′(3,3),Q′(3,3),
∴满足条件的点Q′的坐标为(3,3).
(3,3)

如下图,当PC为对角线时,OQ⊥CP,
易知△OCP是等腰直角三角形,
∴四边形OCQP是正方形,此时Q的坐标为(6,6).



科目:初中数学 来源: 题型:
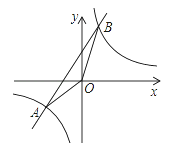
【题目】如图,已知A(﹣2,﹣2)、B(n,4)是一次函数y=kx+b的图象和反比例函数y=![]() 的图象的两个交点.
的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个三位正整数N,各个数位上的数字互不相同且都不为0,若从它的百位、十位、个位上的数字任意选择两个数字组成两位数,所有这些两位数的和等于这个三位数本身,则称这样的三位数N为“公主数”.例如:132,选择百位数字1和十位数字3所组成的两位数为:13和31,选择百位数字1和个位数字2组成的两位数为:12和21,选择十位数字3和个位数字2所组成的两位数为:32和23,因为13+31+12+21+32+23=132,所以132是“公主数”.一个三位正整数,若它的十位数字等于百位数字与个位数字的和,则称这样的三位数为“伯伯数”.
(1)判断123是不是“公主数”?请说明理由.
(2)证明:当一个“伯伯数”![]() 是“公主数”时,则z=2x.
是“公主数”时,则z=2x.
(3)若一个“伯伯数”与132的和能被13整除,求满足条件的所有“伯伯数”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点E、F分别是四边形ABCD边AB、AD上的点,且DE与CF相交于点G.
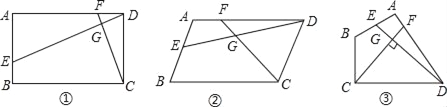
(1)如图①,若AB∥CD,AB=CD,∠A=90°,且ADDF=AEDC,求证:DE⊥CF:
(2)如图②,若AB∥CD,AB=CD,且∠A=∠EGC时,求证:DECD=CFDA:
(3)如图③,若BA=BC=3,DA=DC=4,设DE⊥CF,当∠BAD=90°时,试判断![]() 是否为定值,并证明.
是否为定值,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区有一个景观奇异的天门洞,D点是洞的入口,游人从入口进洞游览后,可经山洞到达山顶的出口凉亭A处观看旅游区风景,最后坐缆车沿索道AB返回山脚下的B处,在同一平面内,若测得斜坡BD的长为100米,坡角∠DBC =10°,在B处测得A的仰角∠ABC=40°,在D处测得A的仰角∠ADF=85°,过D点作地面BE的垂线,垂足为C.
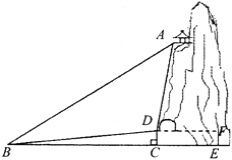
(1)求∠ADB的度数:
(2)过D点作AB的垂线,垂足为G,求DG的长及索道AB的长.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国庆节假日期间,昀昀一家去公园游玩,在一个场所有一个“守株待兔”的游戏,游戏设计者提供了一只兔子和一个有A、B、C、D四个出入口的兔笼,而且笼内的兔子从每个出入口走出兔笼的机会是均等的.游戏规定:①玩家只能将小兔从A、B两个出入口放入;②如果小兔进入笼子后选择从开始进入的出入口离开,则可获得一只价值4元的小兔玩具,否则应付费3元.
(1)画树状图或列表格,写出该游戏的所有可能结果;
(2)昀昀玩该游戏得到小兔玩具的机会有多大?
(3)假设有120人次玩此游戏,估计游戏设计者可赚多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC平分∠DAB,AC2=ABAD,∠ADC=90°,E为AB的中点.

(1)求证:△ADC∽△ACB;
(2)CE与AD有怎样的位置关系?试说明理由;
(3)若AD=4,AB=6,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了了解高峰时段16路公交车从总站乘该路车出行的人数情况,随机抽查了10个班次乘该路车的人数,结果如下:
14,23,16,25,23,28,26,27,23,25.
(1)这组数据的众数为________,中位数为________;
(2)计算这10个班次乘该路车人数的平均数;
(3)如果16路公交车在高峰时段从总站共出车60个班次,根据上面的计算结果,估计在高峰时段从总站乘该路车出行的乘客共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.阜阳市某家快递公司,2017年3月份与5月份完成投递的快递总件数分别为10万件和12.1万件.现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递快递总件数的月平均增长率?
(2) 如果平均每人每月最多可投递快递0.6万件,那么该公司现有的21名快递投递业务员能否完成2017年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com