
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.阜阳市某家快递公司,2017年3月份与5月份完成投递的快递总件数分别为10万件和12.1万件.现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递快递总件数的月平均增长率?
(2) 如果平均每人每月最多可投递快递0.6万件,那么该公司现有的21名快递投递业务员能否完成2017年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
【答案】(1) 快递公司投递快递总件数的月平均增长率为10%;(2)至少需要增加2名业务员.
【解析】试题分析:(1)设该快递公司投递总件数的月平均增长率为x,根据“今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件,现假定该公司每月投递的快递总件数的增长率相同”建立方程,解方程即可;
(2)首先求出今年6月份的快递投递任务,再求出21名快递投递业务员能完成的快递投递任务,比较得出该公司不能完成今年6月份的快递投递任务,进而求出至少需要增加业务员的人数.
试题解析:设该快递公司投递快递总件数的月平均增长率为x,
由题意,得10(1+x)2=12.1,
(1+x)2=1.21,1+x=±1.1,
x1=0.1=10%,x2=-2.1(不合题意,舍去).
答:该快递公司投递总件数的月平均增长率为10%;
(2) ∵0.6×21=12.6(万件),12.1×(1+0.1)=13.31(万件),12.6万件<13.31万件,
∴该公司现有的21名快递投递业务员不能完成今年6月份的快递投递任务.
设需要增加y名业务员,
根据题意,得0.6(y+21)≥13.31,
解得y≥![]() ≈1.183,
≈1.183,
∵y为整数,
∴y≥2.
答:至少需要增加2名业务员.


科目:初中数学 来源: 题型:
【题目】已知:如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于点D,经过B、D两点的⊙O交AB 于点E,交BC于点F,EB为⊙O的直径.
(1)求证:AC是⊙O的切线;
(2)当BC=2,cos∠ABC=![]() 时,求⊙O的半径.
时,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义运算:ab=a(1﹣b).若a,b是方程x2﹣x+![]() m=0(m<0)的两根,则bb﹣aa的值为( )
m=0(m<0)的两根,则bb﹣aa的值为( )
A. 0 B. 1 C. 2 D. 与m有关
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的三个顶点的坐标分别为A(﹣1,3),B(﹣4,0),C(0,0)
⑴画出将△ABC向上平移1个单位长度,再向右平移5个单位长度后得到的△A1B1C1;
⑵画出将△ABC绕原点O顺时针方向旋转90°得到△A2B2O;
⑶在x轴上存在一点P,满足点P到A1与点A2距离之和最小,请直接写出P点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC 中,∠C=90°,BC=3,AC=4.现在要将交ABC 扩充成等腰三角形,且扩充的部分是以AC为直角边的直角三角形,求扩充后等腰三角形的周长.
赵佳同学是这样操作的:如图 1 所示,延长BC 到点 D,使CD=BC,连接AD.所以,△ADB 为符合条件的三角形.则此时△ADB的周长为____________.
请你在图2、图3中再设计两种扩充方案,并直接写出扩充后等腰三角形的周长.
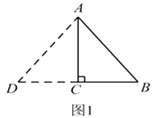
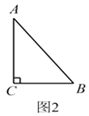
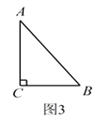
图2的周长:______________;图3的周长:______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰三角形ABC中,AC=BC,分别以BC和AC为直角边向上作等腰直角三角形△BCD和△ACE,AE与BD相交于点F,连接CF并延长交AB于点G.求证:CG垂直平分AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列分解因式正确的是( )
A. m4﹣8m2+64=(m2﹣8)2
B. x4﹣y4=(x2+y2)(x2﹣y2)
C. 4a2﹣4a+1=(2a﹣1)2
D. a(x﹣y)﹣b(y﹣x)=(x﹣y)(a﹣b)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com