
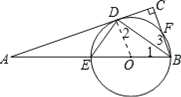
【题目】已知:如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于点D,经过B、D两点的⊙O交AB 于点E,交BC于点F,EB为⊙O的直径.
(1)求证:AC是⊙O的切线;
(2)当BC=2,cos∠ABC=![]() 时,求⊙O的半径.
时,求⊙O的半径.

【答案】(1)见解析;(2)⊙O的半径为![]() .
.
【解析】(1)连结OD,可证得OD∥BC,得到∠ADO=∠C=90°,从而得出结论;
(2)由cos∠ABC=![]() ,得到AB=6,由OD∥BC,得出△AOD∽△ABC,即可求出圆的半径.
,得到AB=6,由OD∥BC,得出△AOD∽△ABC,即可求出圆的半径.
(1)证明:如图,连结OD.
∴OD=OB.∴∠1=∠2.
∵BD平分∠ABC,∴∠1=∠3.
∴∠2=∠3.∴OD∥BC.
∴∠ADO=∠C=90°.∴OD⊥AC.
∵OD是⊙O的半径,
∴AC是⊙O的切线.
(2)解:在Rt△ACB中,∠C=90,BC=2,cos∠ABC=![]() ,
,
∴![]() .
.
设⊙O的半径为r,则AO=6﹣r.
∵OD∥BC,
∴△AOD∽△ABC.
∴![]() ,∴
,∴![]() .
.
解得![]() .
.
∴⊙O的半径为![]() .
.
“点睛”此题主要考查了切线的判定定理与相似三角形的判定和性质定理,此定理是初中阶段非常重要的定理,同学们应正确把握此定理.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10cm,BD⊥AC于点D,BD=8cm.点M从点A出发,沿AC的方向匀速运动,同时直线PQ由点B出发,沿BA的方向匀速运动,运动过程中始终保持PQ∥AC,直线PQ交AB于点P、交BC于点Q、交BD于点F.连接PM,设运动时间为t秒(0<t≤5).线段CM的长度记作y甲,线段BP的长度记作y乙,y甲和y乙关于时间t的函数变化情况如图所示.
(1)由图2可知,点M的运动速度是每秒 cm,当t为何值时,四边形PQCM是平行四边形?在图2中反映这一情况的点是 ;
(2)设四边形PQCM的面积为ycm2,求y与t之间的函数关系式;
(3)是否存在某一时刻t,使S四边形PQCM=![]() S△ABC?若存在,求出t的值;若不存在,说明理由;
S△ABC?若存在,求出t的值;若不存在,说明理由;
(4)连接PC,是否存在某一时刻t,使点M在线段PC的垂直平分线上?若存在,求出此时t的值;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】H7N9型禽流感是一种新型禽流感,于2013年3月底在上海和安徽两地率先发现.H7N9型禽流感是全球首次发现的新亚型流感病毒,其细胞的直径约为0.000000106m,用科学记数法表示这个数是( )
A.0.106×10﹣6m
B.0.106×106m
C.1.06×10﹣7m
D.1.06×107m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某运动队欲从甲、乙两名优秀选手中选一名参加全省射击比赛,该运动队预先对这两名选手进行了8次测试,测得的成绩如表:
次数 | 选手甲的成绩(环) | 选手乙的成绩(环) |
1 | 9.6 | 9.5 |
2 | 9.7 | 9.9 |
3 | 10.5 | 10.3 |
4 | 10.0 | 9.7 |
5 | 9.7 | 10.5 |
6 | 9.9 | 10.3 |
7 | 10.0 | 10.0 |
8 | 10.6 | 9.8 |
根据统计的测试成绩,请你运用所学过的统计知识作出判断,派哪一位选手参加比赛更好?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=60°,∠A=40°.
(1)用尺规作图:作AB的垂直平分线,交AC于点D,交AB于点E(保留作图痕迹,不要求写作法和证明);
(2)求证:BD平分∠CBA.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.阜阳市某家快递公司,2017年3月份与5月份完成投递的快递总件数分别为10万件和12.1万件.现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递快递总件数的月平均增长率?
(2) 如果平均每人每月最多可投递快递0.6万件,那么该公司现有的21名快递投递业务员能否完成2017年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com