
【题目】一个三位正整数N,各个数位上的数字互不相同且都不为0,若从它的百位、十位、个位上的数字任意选择两个数字组成两位数,所有这些两位数的和等于这个三位数本身,则称这样的三位数N为“公主数”.例如:132,选择百位数字1和十位数字3所组成的两位数为:13和31,选择百位数字1和个位数字2组成的两位数为:12和21,选择十位数字3和个位数字2所组成的两位数为:32和23,因为13+31+12+21+32+23=132,所以132是“公主数”.一个三位正整数,若它的十位数字等于百位数字与个位数字的和,则称这样的三位数为“伯伯数”.
(1)判断123是不是“公主数”?请说明理由.
(2)证明:当一个“伯伯数”![]() 是“公主数”时,则z=2x.
是“公主数”时,则z=2x.
(3)若一个“伯伯数”与132的和能被13整除,求满足条件的所有“伯伯数”.
【答案】(1)123不是“公主数”.(2)详见解析;(3)这个“伯伯数”为154或297或583或440.
【解析】
(1)根据“公主数”的定义判断即可;
(2)由题意![]() ,消去y即可解决问题;
,消去y即可解决问题;
(3)设“伯伯数”为![]() ,则y=x+z,则有100x+10y+z+132=110x+11z+11×12=11(10x+z+12),由一个“伯伯数”与132的和能被13整除,可得10x+z+12=13×2或13×3或13×5或13×4,求出整数解即可解决问题;
,则y=x+z,则有100x+10y+z+132=110x+11z+11×12=11(10x+z+12),由一个“伯伯数”与132的和能被13整除,可得10x+z+12=13×2或13×3或13×5或13×4,求出整数解即可解决问题;
(1)解:因为13+31+12+21+32+23=132≠123,
所以123不是“公主数”.
(2)证明:由题意![]() ,
,
∴22(x+x+z+z)=100x+10(x+z)+z,
∴33z=66x,
∴z=2x.
(3)设“伯伯数”为![]() ,则y=x+z,
,则y=x+z,
100x+10y+z+132=110x+11z+11×12=11(10x+z+12),
∵一个“伯伯数”与132的和能被13整除,
∴10x+z+12=13×2或13×3或13×5或13×4
∴![]() 或
或![]() 或
或![]() 或
或![]()
∴这个“伯伯数”为154或297或583或440.


科目:初中数学 来源: 题型:
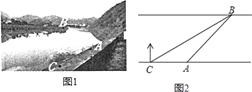
【题目】如图1,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸边点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走60m到达C点,测得点B在点C的北偏东60°方向,如图2.
(1)求∠CBA的度数.
(2)求出这段河的宽(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
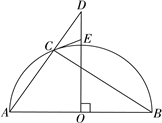
【题目】如图,AB是半圆的直径,过圆心O作AB的垂线,与弦AC的延长线交于点D,点E在OD上![]() .
.
(1)求证:CE是半圆的切线;
(2)若CD=10,![]() ,求半圆的半径.
,求半圆的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
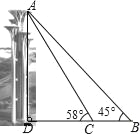
【题目】奥林匹克公园观光塔由五座高度不等、错落有致的独立塔组成.在综合实践活动课中,某小组的同学决定利用测角仪测量这五座塔中最高塔的高度(测角仪高度忽略不计).他们的操作方法如下:如图,他们先在B处测得最高塔塔顶A的仰角为45°,然后向最高塔的塔基直行90米到达C处,再次测得最高塔塔顶A的仰角为58°.请帮助他们计算出最高塔的高度AD约为多少米.(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我校刚刚结束的缤纷体育节上,初三年级参加了60m迎面接力比赛.假设每名同学在跑步过程中是匀速的,且交接棒的时间忽略不计,如图是A、B两班的路程差y(米)与比赛开始至A班先结束第二棒的时间x(秒)之间的函数图象.则B班第二棒的速度为_____米/秒.

查看答案和解析>>
科目:初中数学 来源: 题型:
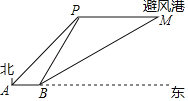
【题目】如图,一艘渔船正以60海里/小时的速度向正东方向航行,在A处测得岛礁P在东北方向上,继续航行1.5小时后到达B处,此时测得岛礁P在北偏东30°方向,同时测得岛礁P正东方向上的避风港M在北偏东60°方向.为了在台风到来之前用最短时间到达M处,渔船立刻加速以75海里/小时的速度继续航行_____小时即可到达.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
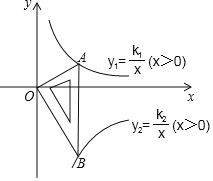
【题目】如图所示是一块含30°,60°,90°的直角三角板,直角顶点O位于坐标原点,斜边AB垂直于x轴,顶点A在函数y1=![]() (x>0)的图象上,顶点B在函数y2=
(x>0)的图象上,顶点B在函数y2=![]() (x>0)的图象上,∠ABO=30°,则
(x>0)的图象上,∠ABO=30°,则![]() = .
= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线![]() :
:![]() 与
与![]() :
:![]() 交于点
交于点![]() ,分别与
,分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() 、
、![]() .
.
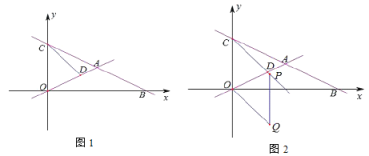
(1)分别求出点![]() 、
、![]() 、
、![]() 的坐标;
的坐标;
(2)若![]() 是线段
是线段![]() 上的点,且
上的点,且![]() 的面积为12,求直线
的面积为12,求直线![]() 的函数表达式;
的函数表达式;
(3)在(2)的条件下,设![]() 是射线
是射线![]() 上的点.
上的点.
①如图2,过点![]() 作
作![]() ,且使四边形
,且使四边形![]() 为菱形,请直接写出点
为菱形,请直接写出点![]() 的坐标;
的坐标;
②在平面内是否存在其它点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?若存在,直接写出点
为顶点的四边形是菱形?若存在,直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017浙江省宁波市)在一次课题学习中,老师让同学们合作编题,某学习小组受赵爽弦图的启发,编写了下面这道题,请你来解一解:
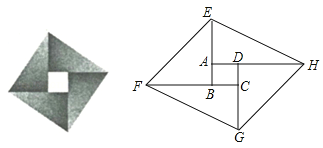
如图,将矩形ABCD的四边BA、CB、DC、AD分别延长至E、F、G、H,使得AE=CG,BF=DH,连接EF,FG,GH,HE.
(1)求证:四边形EFGH为平行四边形;
(2)若矩形ABCD是边长为1的正方形,且∠FEB=45°,tan∠AEH=2,求AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com