
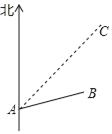
【题目】如图,台风中心位于点A,并沿东北方向AC移动,已知台风移动的速度为50千米/时,受影响区域的半径为130千米,B市位于点A的北偏东75°方向上,距离A点240千米处.
(1)说明本次台风会影响B市;
(2)求这次台风影响B市的时间.
【答案】(1)见解析;(2)2小时.
【解析】
(1)作BD⊥AC于点D,在Rt△ABD中,利用含30°角的直角三角形的性质求出BD的长与130千米相比较即可.
(2)以B为圆心,以130为半径作圆交AC于E,F两点,根据垂径定理即可求出BE=BF=130,然后由勾股定理求得EF的长度,进而求出台风影响B市的时间.
解:(1)如图,作BD⊥AC于点D.
在Rt△ABD中,由条件知,AB=240,∠BAC=75°﹣45°=30°,
∴BD=240×![]() =120<130,
=120<130,
∴本次台风会影响B市.
(2)如图,以点B为圆心,以130为半径作圆交AC于E,F,
若台风中心移动到E时,台风开始影响B市,台风中心移动到F时,台风影响结束.
由(1)得BD=240,由条件得BE=BF=130,
∴EF=![]() =100,
=100,
∴台风影响的时间t=![]() =2(小时).
=2(小时).
故B市受台风影响的时间为2小时.


 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】利民商场经营某种品牌的T恤,购进时的单价是300元,根据市场调查:在一段时间内,销售单价是400元时,销售量是60件,销售单价每涨10元,销售量就减少1件.设这种T恤的销售单价为x元(x>400)时,销售量为y件、销售利润为W元.
(1)请分别用含x的代数式表示y和W(把结果填入下表):
销售单价(元) | x |
销售量y(件) | |
销售利润W(元) |
(2)该商场计划实现销售利润10000元,并尽可能增加销售量,那么x的值应当是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
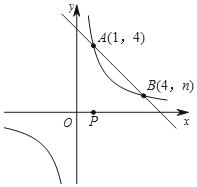
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象交于A(1,4),B(4,n)两点.
的图象交于A(1,4),B(4,n)两点.
(1)求反比例函数和一次函数的解析式;
(2)直接写出当x>0时,kx+b<![]() 的解集.
的解集.
(3)点P是x轴上的一动点,试确定点P并求出它的坐标,使PA+PB最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
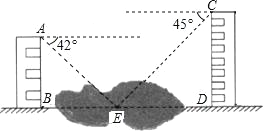
【题目】如图,两幢建筑物AB和CD,AB⊥BD,CD⊥BD,AB=15m,CD=20m.AB和CD之间有一景观池,小双在A点测得池中喷泉处E点的俯角为42°,在C点测得E点的俯角为45°,点B、E、D在同一直线上.求两幢建筑物之间的距离BD.(结果精确到0.1m)(参考数据:sin42°=0.67,cos42°=0.74,tan42°=0.90)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c的图象经过点(0,3),(x1,0),其中,2<x1<3,对称轴为x=1,则下列结论:①2a﹣b=0; ②x(ax+b)≤a+b;③方程ax2+bx+c﹣3=0的两根为x1'=0,x2'=2;④﹣3<a<﹣1.其中正确的是( )
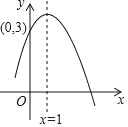
A. ②③④B. ①②③C. ②④D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某日的钱塘江观潮信息如表:

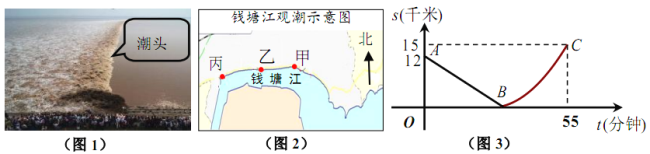
按上述信息,小红将“交叉潮”形成后潮头与乙地之间的距离![]() (千米)与时间
(千米)与时间![]() (分钟)的函数关系用图3表示,其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点
(分钟)的函数关系用图3表示,其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点![]() ,点
,点![]() 坐标为
坐标为![]() ,曲线
,曲线![]() 可用二次函数
可用二次函数![]() (
(![]() ,
,![]() 是常数)刻画.
是常数)刻画.
(1)求![]() 的值,并求出潮头从甲地到乙地的速度;
的值,并求出潮头从甲地到乙地的速度;
(2)11:59时,小红骑单车从乙地出发,沿江边公路以![]() 千米/分的速度往甲地方向去看潮,问她几分钟后与潮头相遇?
千米/分的速度往甲地方向去看潮,问她几分钟后与潮头相遇?
(3)相遇后,小红立即调转车头,沿江边公路按潮头速度与潮头并行,但潮头过乙地后均匀加速,而单车最高速度为![]() 千米/分,小红逐渐落后,问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度
千米/分,小红逐渐落后,问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度![]() ,
,![]() 是加速前的速度).
是加速前的速度).
查看答案和解析>>
科目:初中数学 来源: 题型:
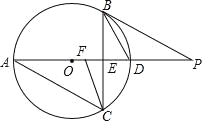
【题目】如图,已知△ABC内接于⊙O,直径AD⊥BC于E,点F是OE的中点,且BD∥CF.
(1)若BD=3![]() ,求BC的长.
,求BC的长.
(2)若BD平分∠CBP,求证:ABBD=BPAF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,以△ABC的边AB为直径作⊙O,交AC边于点E,BD平分∠ABE交AC于F,交⊙O于点D,且∠BDE=∠CBE.
(1)求证:BC是⊙O的切线;
(2)延长ED交直线AB于点P,如图2,若PA=AO,DE=3,DF=2,求![]() 的值及AO的长.
的值及AO的长.
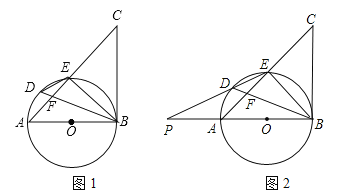
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com